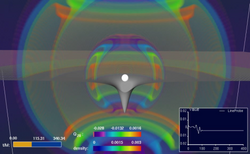
Động đen, là một vùng không - thời gian có một trường hấp dẫn mạnh đến nỗi không có vật chất nói chung chiếm khối lượng và không gian nhất định hoặc các bức xạ và ánh sáng nào có thể thoát ra ngoài.[4][5][6] Thuyết tương đối rộng tiên đoán một lượng vật chất với khối lượng đủ lớn nằm trong phạm vi đủ nhỏ sẽ làm biến dạng không thời gian để trở thành lỗ đen. Xung quanh lỗ đen là một mặt xác định bởi phương trình toán học gọi là chân trời sự kiện, mà tại đó khi vật chất vượt qua nó sẽ không thể thoát ra ngoài lỗ đen được. Lỗ đen gọi là "đen" bởi vì nó hấp thụ mọi bức xạ và vật chất hút qua chân trời sự kiện, giống như một vật đen tuyệt đối trong nhiệt động lực học; nó cũng không phải là một loại "lỗ" hay "hố" nào mà là vùng không thời gian không để cho một thứ gì thoát ra.[7][8] Lý thuyết trường lượng tử trong không thời gian cong tiên đoán tại chân trời sự kiện lỗ đen có phát ra bức xạ giống như vật đen có nhiệt độ nhất định phát ra bức xạ nhiệt. Nhiệt độ này tỉ lệ nghịch với khối lượng của lỗ đen, khiến cho rất khó quan sát được bức xạ này đối với các lỗ đen có khối lượng sao hay trung bình.
Trong thế kỷ 18, John Michell và Pierre-Simon Laplace từng xét đến vật thể có trường hấp dẫn mạnh mô tả bởi cơ học cổ điển khiến cho ánh sáng không thể thoát ra. Lý thuyết hiện đại đầu tiên về đặc điểm của lỗ đen nêu bởi Karl Schwarzschild năm 1916 khi ông tìm ra nghiệm chính xác đầu tiên cho phương trình trường Einstein,[9] mặc dù ý nghĩa vật lý và cách giải thích về vùng không thời gian mà không thứ gì có thể thoát được do David Finkelstein nêu ra đầu tiên vào năm 1958.[10] Trong một thời gian dài, các nhà vật lý coi nghiệm Schwarzschild là miêu tả toán học thuần túy. Cho đến thập niên 1960, những nghiên cứu lý thuyết mới chỉ ra rằng lỗ đen hình thành theo những tiên đoán chặt chẽ của thuyết tương đối tổng quát. Khi các nhà thiên văn học phát hiện ra các sao neutron, pulsar và Cygnus X-1 - một lỗ đen trong hệ sao đôi, thì những tiên đoán về quá trình suy sụp hấp dẫn trở thành hiện thực, và khái niệm lỗ đen cùng với các thiên thể đặc chuyển thành lý thuyết miêu tả những thực thể đặc biệt này trong vũ trụ.
Theo lý thuyết, lỗ đen khối lượng sao hình thành từ sự suy sụp hấp dẫn của những sao có khối lượng rất lớn trong giai đoạn cuối của quá trình tiến hóa. Sau khi hình thành, chúng tiếp tục thu hút vật chất từ môi trường xung quanh, và khối lượng tăng dần lên theo thời gian. Cùng với quá trình hòa trộn và sáp nhập hai hay nhiều lỗ đen mà tồn tại những lỗ đen khổng lồ với khối lượng từ vài triệu cho đến hàng chục tỷ lần khối lượng Mặt Trời. Các dự án khảo sát cho thấy đa phần tại trung tâm thiên hà lớn đều tồn tại ít nhất một lỗ đen khổng lồ.
Mặc dù theo định nghĩa nó là vật thể đen hoàn toàn hay vô hình, sự tồn tại của lỗ đen có thể suy đoán thông qua tương tác của nó với môi trường vật chất xung quanh và bức xạ như ánh sáng. Vật chất rơi vào lỗ đen hình thành lên vùng bồi tụ,[11] ở đây vật chất va chạm và ma sát với nhau, trở thành trạng thái plasma phát ra bức xạ cường độ lớn; khiến môi trường bao quanh lỗ đen trở thành một trong những vật thể sáng nhất trong vũ trụ. Nếu có một ngôi sao quay quanh lỗ đen, hình dáng và chu kỳ quỹ đạo của nó cho phép các nhà thiên văn tính ra được khối lượng của lỗ đen và khoảng cách đến nó. Những dữ liệu này giúp họ phân biệt được thiên thể đặc là lỗ đen hay sao neutron... Theo cách này, nhiều lỗ đen được phát hiện ra nằm trong hệ sao đôi, và tại trung tâm Ngân Hà có một lỗ đen khổng lồ với khối lượng xấp xỉ 4,4 triệu lần khối lượng Mặt Trời.[12]
Lý thuyết về lỗ đen, nơi có trường hấp dẫn mạnh tập trung trong vùng không thời gian nhỏ, là một trong số những lý thuyết cần sự tổng hợp của thuyết tương đối tổng quát miêu tả lực hấp dẫn với Mô hình chuẩn của cơ học lượng tử. Và hiện nay, các nhà lý thuyết vẫn đang trên con đường xây dựng thuyết hấp dẫn lượng tử để có thể miêu tả vùng kì dị tại trung tâm lỗ đen.[13]
Sự kiện đo được trực tiếp đầu tiên về sóng hấp dẫn do nhóm LIGO đăng báo ngày 11 tháng 2 năm 2016 cũng đã chứng minh trực tiếp sự tồn tại hệ hai lỗ đen khối lượng sao quay quanh nhau và cuối cùng sáp nhập để tạo thành một lỗ đen quay khối lượng lớn hơn.[14]
| Thuyết tương đối rộng |
|---|
 '"`UNIQ--postMath-00000001-QINU`"' |
|
Giới thiệu · Mô hình Toán học Tham khảo · Kiểm chứng · Lịch sử |
|
Các khái niệm cơ sở |
|
Hiệu ứng và hệ quả |
|
Các lý thuyết phát triển |
|
Nhà vật lý Einstein · Lorentz · Hilbert · Poincare · Schwarzschild · Sitter · Reissner · Nordström · Weyl · Eddington · Friedman · Milne · Zwicky · Lemaître · Gödel · Wheeler · Robertson · Bardeen · Walker · Kerr · Chandrasekhar · Ehlers · Penrose · Hawking · Taylor · Hulse · Stockum · Taub · Newman · Khâu Thành Đồng · Thorne khác |
Lịch sử nghiên cứu

Ý tưởng về một vật thể khối lượng lớn khiến cho ánh sáng không thể thoát ra khỏi nó lần đầu tiên nêu bởi John Michell trong một lá thư gửi tới Henry Cavendish ở Hội Hoàng gia năm 1783:
"Nếu bán kính của một khối cầu với cùng khối lượng như Mặt Trời, nhỏ hơn bán kính của Mặt Trời với tỉ lệ 500 trên 1, một vật rơi từ điểm xa vô cùng về phía nó sẽ thu được vận tốc tại lúc chạm bề mặt khối cầu lớn hơn tốc độ ánh sáng; và giả sử là ánh sáng bị hút với cùng một lực tỉ lệ theo khối lượng quán tính, giống như những vật khác, mọi ánh sáng phát ra từ bề mặt của khối cầu sẽ quay trở lại nó do lực hút hấp dẫn của khối cầu."
— John Michell[15]
Năm 1796, Pierre-Simon Laplace cũng nêu ra ý niệm này trong ấn bản lần thứ nhất và thứ hai của cuốn sách Exposition du système du Monde (nhưng nó đã bị bỏ đi trong những lần ấn bản sau).[16][17] Những "ngôi sao" tối này sau đó bị lãng quên vào thế kỷ 19, do đa số các nhà vật lý nghĩ rằng ánh sáng không có khối lượng và không thể bị ảnh hưởng bởi lực hấp dẫn.[18]
Thuyết tương đối rộng
Năm 1915, Albert Einstein hoàn thiện thuyết tương đối rộng, mà trước đó ông đã tiên đoán được trường hấp dẫn làm lệch đường đi của tia sáng. Chỉ hai tháng sau khi công bố lý thuyết, nhà thiên văn học Karl Schwarzschild tìm thấy nghiệm chính xác đầu tiên cho phương trình trường Einstein, nghiệm miêu tả trường hấp dẫn cho một khối lượng điểm hoặc khối cầu phân bố đều trong "hệ tọa độ cầu" bốn chiều.[9] Vài tháng sau Schwarzschild, Johannes Droste, lúc đó là sinh viên của Hendrik Lorentz, cũng độc lập đưa ra nghiệm tương tự cho khối lượng điểm và khảo cứu thêm những tính chất của nghiệm này.[19][20] Nghiệm này có một tính chất kỳ lạ mà ngày nay gọi là bán kính Schwarzschild, biên giới mà tại đó không thời gian miêu tả bởi tọa độ Schwarzschild trở lên gián đoạn, hay mặt biên này chia hệ tọa độ làm hai vùng tách biệt nhau; và lúc đó các nhà vật lý nghĩ rằng phương trình trường Einstein không miêu tả tốt tại bán kính này. Họ đã không hiểu thấu đáo bản chất của bề mặt này khi đó. Năm 1924, Arthur Eddington chứng minh được bán kính này biến mất cũng như không thời gian sẽ vẫn liên tục nếu ông chọn một hệ tọa độ khác (xem hệ tọa độ Eddington–Finkelstein), đồng thời độ cong không thời gian tại bán kính Schwarzschild có giá trị hữu hạn vẫn không đổi giữa các hệ tọa độ. Mặc dù phải đợi cho đến tận năm 1933, Georges Lemaître mới nhận ra rằng điều này có nghĩa là kỳ dị tại bán kính Schwarzschild là một kỳ dị toán học không có ý nghĩa vật lý.[21]
Năm 1931, Subrahmanyan Chandrasekhar sử dụng thuyết tương đối hẹp cho chất khí Fermi của vật thể không tự quay - hay ngày nay là sao lùn trắng cấu tạo bằng vật chất chống đỡ bởi áp suất từ các electron - tính ra được nếu trên một khối lượng xấp xỉ 1,4 khối lượng Mặt Trời (ngày nay gọi là giới hạn Chandrasekhar) thì vật thể sẽ không tồn tại ổn định.[22] Kết quả của ông bị một số nhà vật lý cùng thời phản đối như Eddington và Lev Landau, mà ông cho rằng có một cơ chế chưa biết làm dừng quá trình suy sụp lại.[23] Họ đã đúng một phần: sao lùn trắng có khối lượng hơi lớn hơn giới hạn Chandrasekhar sẽ suy sụp hấp dẫn thành sao neutron,[24] khi proton bị nén hấp dẫn mạnh kết hợp với electron thành neutron, mà vật chất neutron có thể ổn định nhờ nguyên lý loại trừ Pauli. Nhưng vào năm 1939, Robert Oppenheimer cùng hai người khác chứng minh rằng, với ước tính chặt chẽ hơn sau này, nếu các sao neutron có khối lượng xấp xỉ trên 3 lần khối lượng Mặt Trời (giới hạn Tolman–Oppenheimer–Volkoff) thì chúng cũng không thể tồn tại ổn định và nhanh chóng suy sụp hấp dẫn như Chandrasekhar từng tiên đoán, và họ kết luận rằng không một định luật vật lý nào có thể ngăn cản những loại sao khối lượng lớn suy sụp hấp dẫn.[25][26]
Oppenheimer và đồng nghiệp giải thích kỳ dị tại bán kính Schwarzschild như là một bong bóng với thời gian ngừng lại tại biên này. Quan điểm này chỉ đúng với người quan sát đứng ở bên ngoài bán kính Schwarzschild, nhưng không đúng đối với một người rơi qua biên và hướng về tâm lỗ đen. Bởi vì tính chất này, các nhà vật lý từng gọi ngôi sao suy sụp hấp dẫn thành "ngôi sao bị đóng băng",[27] bởi vì quan sát viên đứng ở xa bên ngoài sẽ thấy hình ảnh của vật rơi vào lỗ đen như dừng lại tại phía ngoài sát biên giới của bán kính Schwarzschild, và nếu vật có phát ra ánh sáng thì ánh sáng đó sẽ dần dần mờ đi rồi tắt hẳn, tuy vậy đối với vật thể rơi vào tâm lỗ đen nó sẽ chỉ mất một thời gian hữu hạn để đi qua chân trời sự kiện.[28][29]
Thời kỳ vàng
Năm 1958, David Finkelstein miêu tả bề mặt Schwarzschild như một chân trời sự kiện, "một màng tưởng tượng không phương hướng hoàn hảo: những ảnh hưởng nhân quả chỉ có thể đi qua mặt theo một hướng nhất định".[30] Nhận xét này không mâu thuẫn với kết quả của Oppenheimer và đồng nghiệp, nhưng cho phép mở rộng chúng sang quan điểm của quan sát viên đang rơi vào trong lỗ đen. Hệ tọa độ của Finkelstein mở rộng nghiệm Schwarzschild miêu tả những người rơi vào lỗ đen sẽ thấy cấu trúc không thời gian biến đổi như thế nào trong quá trình rơi xuống. Martin Kruskal ngay sau đó nêu ra phương pháp mở rộng đầy đủ hoàn toàn cho nghiệm này.[31]
Những kết quả này là sự khởi đầu cho "thời kỳ vàng của thuyết tương đối rộng", do Kip Thorne đặt tên, đánh dấu thời điểm thuyết tương đối tổng quát và vật lý lỗ đen trở thành một trong những hướng nghiên cứu chính của vật lý học hiện đại.[32] Trong thời gian này có thêm sự khám phá ra pulsar năm 1967,[33][34] mà sau đó vào năm 1969, Antony Hewish chỉ ra đây là những sao neutron quay rất nhanh quanh trục của chúng.[35] Cho đến tận thời điểm đó, các nhà vật lý coi sao neutron, giống như lỗ đen, là những mẫu hình kỳ lạ của thuyết tương đối rộng; nhưng việc phát hiện ra các pulsar có những tính chất vật lý liên quan đến mô hình lý thuyết cũng chứng tỏ những thiên thể đặc thú vị khác phải hình thành từ sự suy sụp hấp dẫn.
Trong thời gian này, thêm một số nghiệm chính xác miêu tả lỗ đen được tìm ra. Năm 1963, Roy Kerr tìm được nghiệm chính xác cho một lỗ đen đứng yên quay quanh trục của nó. Hai năm sau, Ezra Newman tổng quát hóa mêtric Kerr cho lỗ đen quay và mang điện tích.[36] Và những nghiên cứu tiếp sau đó của Werner Israel,[37] Brandon Carter,[38][39] và David Robinson[40] dần mang lại định lý lỗ đen "không có tóc", phát biểu rằng nghiệm chính xác miêu tả lỗ đen đứng yên chỉ cần ba tham số trong mêtric Kerr–Newman; khối lượng, động lượng quay, và điện tích là đủ.[41]
Ban đầu, các nhà vật lý nghĩ rằng những đặc điểm kì lạ của các mêtric miêu tả lỗ đen là do cách lựa chọn các tính chất đối xứng trong quá trình tìm lời giải cho phương trình trường Einstein, và do vậy miền kì dị xuất hiện chỉ mang tính nhân tạo và không mang ý nghĩa vật lý trong mọi tình huống. Quan điểm này được các nhà vật lý Vladimir Belinsky, Isaak Khalatnikov, và Evgeny Lifshitz ủng hộ khi họ cố gắng chứng minh không tồn tại các kì dị trong những tình huống nói chung.[42] Tuy nhiên, vào cuối những năm 1960 Roger Penrose[43] và Stephen Hawking sử dụng kĩ thuật toàn cục để chứng minh rằng mọi metric miêu tả lỗ đen đều xuất hiện kì dị trong đó.[44]
Những nghiên cứu của James Bardeen, Jacob Bekenstein, Carter, và Hawking trong đầu thập niên 1970 đã khai sinh ra ngành nhiệt động lực học lỗ đen.[45] Những định luật này miêu tả các tính chất của lỗ đen theo những đặc điểm tương tự như các định luật của nhiệt động lực học bởi liên hệ giữa khối lượng và năng lượng, diện tích chân trời sự kiện với entropy, và hấp dẫn bề mặt với nhiệt độ. Vào năm 1974, Hawking hoàn thiện các liên hệ này khi chứng minh rằng lý thuyết trường lượng tử trong không thời gian cong tiên đoán các lỗ đen có phát ra các bức xạ - giống như vật đen ở nhiệt độ xác định phát ra bức xạ nhiệt - tỷ lệ với hấp dẫn bề mặt của lỗ đen.[46]
Thuật ngữ "lỗ đen" do nhà vật lý John Wheeler lần đầu tiên nhắc tới trong một bài giảng năm 1967. Mặc dù cộng đồng khoa học coi ông là người khai sinh ra thuật ngữ này, nhưng ông luôn nói rằng ông lấy tên gọi này từ một người khác gợi ra ý tưởng cho ông. Trước đó, bài báo đầu tiên sử dụng thuật ngữ lỗ đen trong bài viết "Black Holes in Space" của nhà báo Ann Ewing, đề ngày 18 tháng 1 năm 1964, đọc trong hội nghị của Hiệp hội Mỹ vì sự phát triển khoa học AAAS.[47] Sau khi Wheeler phổ biến thuật ngữ này ra, nó nhanh chóng được giới khoa học và công chúng sử dụng rộng rãi.
Các tính chất và cấu trúc
Định lý không có tóc phát biểu rằng, lúc đạt đến điều kiện ổn định sau khi hình thành, một lỗ đen đứng yên chỉ cần ba tham số vật lý độc lập để miêu tả nó: khối lượng, điện tích, và mô men động lượng.[41][48] Bất kỳ hai lỗ đen nào mà có cùng những tính chất vật lý này, hay mỗi cặp ba tham số bằng nhau, thì không thể phân biệt được với nhau theo cơ học cổ điển (hay là phi-lượng tử).
Những tính chất này đặc biệt vì một người đứng ở bên ngoài lỗ đen sẽ đo được ba tham số này. Ví dụ, một hố đen mang điện tích sẽ đẩy những lỗ đen khác mang điện tích cùng dấu khác giống như trong tĩnh điện học cổ điển. Tương tự, tổng khối lượng (theo nghĩa năng lượng + khối lượng), khối lượng ADM, bên trong lỗ đen có thể tìm được bằng cách sử dụng định luật Gauss cho hấp dẫn hoặc quan sát quỹ đạo của các vật thể quay quanh nó.[49] Và đối với mô men động lượng, một người ở xa có thể xác định được thông qua hiệu ứng kéo hệ quy chiếu gây bởi sự tự quay của nó (trường hấp dẫn từ).[50]
Khi một vật rơi vào lỗ đen, bất kỳ thông tin nào về hình dạng, phân bố điện tích... của vật đó hoàn toàn biến mất đối với quan sát viên đứng ở ngoài xa lỗ đen. Tính chất của chân trời sự kiện trong tình huống này như một hệ tiêu tán tương tự với một màng hai chiều, trên đó hình dung tồn tại chất lỏng có ma sát mang điện tích và dẫn điện, trong không thời gian bốn chiều—hay mô hình màng về lỗ đen.[51] Đặc điểm này khác với các lý thuyết trường khác của vật lý học như trường điện từ cổ điển, mà chúng không có ma sát hay độ dẫn điện ở cấp vi mô, bởi vì chúng tuân theo đối xứng thời gian, trong khi một vật rơi vào lỗ đen thì không thể bay trở ra được. Bởi vì trạng thái ổn định sau khi hình thành lỗ đen chỉ cần miêu tả bởi ba tham số, không có cách nào để tránh khỏi mất thông tin về những điều kiện ban đầu: trường hấp dẫn và điện từ của lỗ đen cho rất ít thông tin về trạng thái trước khi hình thành nó và về những cái rơi vào nó. Ví dụ, một vệ tinh nhân tạo hình lập phương rơi vào lỗ đen thì chúng ta chỉ biết được, về nguyên lý, lỗ đen tăng thêm khối lượng bằng khối lượng vệ tinh còn không thể biết được vệ tinh có hình lập phương hay hình trụ tròn. Ngoài ra, có rất nhiều dạng thông tin vật lý bị mất, những đại lượng không thể đo được bởi một người đứng ở xa bên ngoài chân trời sự kiện, bao gồm các đại lượng tuân theo định luật bảo toàn, số lượng tử, số baryon và số lepton, số hạt mang điện tích... Những điều này được phát biểu toán học chi tiết hơn ở nghịch lý thông tin bị mất trong lỗ đen.[52][53]
Tính chất vật lý
Loại lỗ đen đơn giản nhất là chỉ có khối lượng mà không có điện tích hay quay quanh trục của nó. Những lỗ đen này được miêu tả bằng mêtric Schwarzschild mang tên Karl Schwarzschild, người đã tìm ra lời giải chính xác cho phương trình của thuyết tương đối tổng quát năm 1916.[9] Theo định lý Birkhoff, đây là nghiệm miêu tả không thời gian vùng chân không bên ngoài một khối vật chất có dạng đối xứng cầu.[54] Điều này có nghĩa là không có sự khác biệt giữa trường hấp dẫn của một lỗ đen với những vật thể khác với bán kính lớn hơn dạng cầu có cùng khối lượng.[55] Hình ảnh phổ biến trong kiến thức đại chúng về một lỗ đen đó là nó hút mọi thứ xung quanh về phía chân trời sự kiện của nó; xa bên ngoài lỗ đen, trường hấp dẫn do lỗ đen làm cong không thời gian quanh nó trở lên yếu đi và giống với trường hấp dẫn của vật thể cầu cùng khối lượng.[56]
Cũng có những nghiệm tổng quát hơn miêu tả gần với thực tế của lỗ đen. Lỗ đen dạng cầu mang điện tích được miêu tả bởi mêtric Reissner–Nordström, tuy vậy trong vũ trụ đa số các lỗ đen là trung hòa về điện. Lỗ đen đứng yên và quay quanh trục miêu tả theo mêtric Kerr. Mô hình tổng quát nhất cho lỗ đen đứng yên, quay quanh trục và mang điện tích đó là mêtric Kerr–Newman, do Erza Newman tìm ra.[57]
Trong thuyết tương đối rộng, khối lượng lỗ đen có thể nhận một giá trị dương bất kỳ, nhưng giá trị điện tích và mô men động lượng bị giới hạn theo giá trị khối lượng của nó. Trong đơn vị Planck, tổng điện tích Q và mô men động lượng toàn phần J thỏa mãn bất đẳng thức
- '"`UNIQ--postMath-00000002-QINU`"'
| Không quay (J = 0) | Quay (J ≠ 0) | |
| Trung hòa (Q = 0) | Schwarzschild | Kerr |
| Điện tích (Q ≠ 0) | Reissner–Nordström | Kerr–Newman |
với M là khối lượng lỗ đen. Những lỗ đen có giá trị các tham số thỏa mãn dấu bằng của bất đẳng thức gọi là các lỗ đen cực trị. Cũng tồn tại những nghiệm của phương trình trường Einstein vi phạm bất đẳng thức này, nhưng trong nghiệm lại không có một chân trời sự kiện. Các nhà vật lý lý thuyết gọi những nghiệm này là kì dị trần trụi, tức là điểm kì dị mà người ở xa bên ngoài nhìn thấy được nó hay không bị ngăn cản bởi một chân trời sự kiện.[58][59] Nhà toán lý Roger Penrose đưa ra phỏng đoán kiểm duyệt vũ trụ khi ông cho rằng, ngoài kì dị Big Bang, thì không tồn tại kì dị trần trụi nào xuất hiện sau quá trình suy sụp hấp dẫn của vật chất trong vũ trụ.[60][61] Các mô phỏng trên siêu máy tính cho kết quả ủng hộ giả thuyết này.[62]
Do cường độ tương đối lớn của lực điện từ, các lỗ đen hình thành từ sự suy sụp hấp dẫn của các sao sẽ trung hòa về điện. Cũng có lỗ đen sau khi hình thành chúng quay rất nhanh quanh trục, một tính chất có thể suy ra từ định luật bảo toàn mô men động lượng. Có khả năng trong hệ hai thiên thể, GRS 1915+105 với một nguồn tia X mạnh chứa lỗ đen,[63] mà các nhà thiên văn đo được vận tốc tự quay của nó đạt xấp xỉ giá trị cực đại theo tính toán trên lý thuyết cho một lỗ đen.
| Lớp | Khối lượng | Kích thước |
|---|---|---|
| Lỗ đen siêu khối lượng[64] | ~106–1010 M |
~0,001–400 AU |
| Lỗ đen khối lượng trung gian[65] | ~103–105 M |
~103 km ≈ RTrái Đất |
| Lỗ đen khối lượng sao[64] | ~10–102 M |
~30 km |
| Lỗ đen siêu nhỏ | đến ~MMặt Trăng | up to ~0,1 mm |
Trong vật lý thiên văn, lỗ đen còn được phân loại theo khối lượng của chúng không kể tới hai tham số kia; ngoài cách phân loại theo tính chất là khối lượng, mô men động lượng J hay điện tích Q. Kích thước của một lỗ đen, như được xác định bằng bán kính của chân trời sự kiện, hay bán kính Schwarzschild, tỉ lệ với khối lượng M của nó
- '"`UNIQ--postMath-00000003-QINU`"'
với rS là bán kính Schwarzschild và M![]() là khối lượng Mặt Trời.[66] Liên hệ này chỉ đúng chính xác cho lỗ đen không quay quanh trục và không có điện tích; đối với lỗ đen tổng quát nói chung giá trị này có thể lớn gấp 2 lần.
là khối lượng Mặt Trời.[66] Liên hệ này chỉ đúng chính xác cho lỗ đen không quay quanh trục và không có điện tích; đối với lỗ đen tổng quát nói chung giá trị này có thể lớn gấp 2 lần.
Đến 2013, lỗ đen có khối lượng nhỏ nhất từng đo được là GRO J0422+32 với xấp xỉ 5 M![]() ,[67] mặc dù năm 2008 các nhà khoa học NASA công bố phát hiện thiên thể XTE J1650-500 có khối lượng xấp xỉ 3,8 lần khối lượng Mặt Trời[68] nhưng sau đó các kết quả đo đạc lại chứng tỏ nó có khối lượng ít nhất 5-10 khối lượng Mặt Trời.[69] Một số lỗ đen có khối lượng lớn nhất bao gồm: tại trung tâm thiên hà NGC 1277, cách Trái Đất 220 x 106 ly với giá trị 17 x 109 M
,[67] mặc dù năm 2008 các nhà khoa học NASA công bố phát hiện thiên thể XTE J1650-500 có khối lượng xấp xỉ 3,8 lần khối lượng Mặt Trời[68] nhưng sau đó các kết quả đo đạc lại chứng tỏ nó có khối lượng ít nhất 5-10 khối lượng Mặt Trời.[69] Một số lỗ đen có khối lượng lớn nhất bao gồm: tại trung tâm thiên hà NGC 1277, cách Trái Đất 220 x 106 ly với giá trị 17 x 109 M![]() ;[70] hệ hai lỗ đen OJ 287 có khối lượng lần lượt 100 x 106 và 17 ~ 18 x 109 M
;[70] hệ hai lỗ đen OJ 287 có khối lượng lần lượt 100 x 106 và 17 ~ 18 x 109 M![]() nằm cách Trái Đất 3,5 x 109 ly;[71] tại trung tâm thiên hà NGC 4889 cách Trái Đất 308 x 106 ly với khối lượng 21 x 109 M
nằm cách Trái Đất 3,5 x 109 ly;[71] tại trung tâm thiên hà NGC 4889 cách Trái Đất 308 x 106 ly với khối lượng 21 x 109 M![]() (với độ bất định 6 ~ 37 x 109 M
(với độ bất định 6 ~ 37 x 109 M![]() ).[72]
).[72]
Chân trời sự kiện
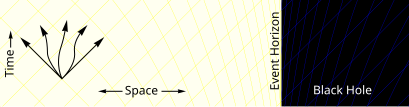 Một hạt ở xa bên ngoài lỗ đen có thể chuyển động theo hướng bất kỳ, như minh họa bởi các mũi tên. Nó chỉ bị giới hạn bởi tốc độ ánh sáng.[73] |
 Càng gần lỗ đen, không thời gian bao quanh nó bị uốn cong mạnh hơn (thể hiện bởi nón ánh sáng theo lưới màu vàng nhạt và xanh nhạt). Bắt đầu có nhiều đường đi của hạt dẫn về lỗ đen hơn các đường di chuyển tự do.[Ct 1] |
 Bên trong chân trời sự kiện, mọi đường đi của hạt hướng về tâm lỗ đen và hạt không thể thoát ra được. |
Bề mặt biểu kiến của lỗ đen được định nghĩa tại chân trời sự kiện—biên giới trong không thời gian mà khi vượt qua nó vật chất và bức xạ chỉ có thể đi về tâm lỗ đen. Không một thứ gì, ngay cả ánh sáng, có thể từ trong lỗ đen thoát ra ngoài chân trời sự kiện. Chân trời sự kiện được định nghĩa như vậy bởi vì đối với những sự kiện xảy ra bên trong nó, mọi thông tin của sự kiện không thể vượt ra ngoài để đến được một quan sát viên ở xa lỗ đen, khiến cho người đó không thể biết được bên trong nó là như thế nào.[75]
Thuyết tương đối tổng quát tiên đoán khối lượng làm uốn cong không thời gian khiến cho quỹ đạo (hay đường trắc địa) của hạt hoặc của photon bị lệch hướng về phía khối lượng đó.[76] Tại chân trời sự kiện của lỗ đen, độ cong không thời gian trở lên rất lớn khiến cho không một đường nào có thể đi ra khỏi lỗ đen.
Đối với một người ở rất xa, họ sẽ thấy những đồng hồ càng gần lỗ đen chạy chậm hơn so với những đồng hồ nằm xa hơn.[77] Do hiệu ứng này, gọi là sự giãn thời gian do hấp dẫn, quan sát viên ở xa thấy một vật rơi vào lỗ đen dường như chuyển động chậm dần đi khi nó đến gần chân trời sự kiện, và cần một thời gian vô hạn để đến tới chân trời này.[78] Nếu như vật phát ra ánh sáng xanh, thì quan sát viên ở ngoài sẽ thấy ánh sáng càng đỏ hơn và mờ hơn khi vật tiến đến chân trời sự kiện, một hiệu ứng mà các nhà vật lý gọi là dịch chuyển đỏ do hấp dẫn.[79] Tuy đối với người ở xa tưởng chừng như vật đó rơi đến và đứng yên tại nơi gần biên giới lỗ đen, nhưng đối với vật thể nó chỉ cần thời gian hữu hạn để vượt qua chân trời lỗ đen.[28][29]
Hình dạng của chân trời sự kiện lỗ đen luôn luôn có dạng xấp xỉ hình cầu.[Ct 2][82] Đối với lỗ đen đứng yên không quay, biên giới lỗ đen có dạng hình cầu. Nếu lỗ đen đứng yên và quay quanh trục thì nó có dạng hình phỏng cầu và theo các phương trình toán học nó có hai chân trời sự kiện.[83]
Vùng kì dị
Một đặc điểm của thuyết tương đối tổng quát đó là trong các nghiệm miêu tả lỗ đen, tại trung tâm của nó có một vùng kì dị hấp dẫn, nơi độ cong không thời gian có giá trị vô hạn (hay kì dị độ cong).[84] Đối với lỗ đen không quay, vùng này chỉ là một điểm r = 0, và đối với lỗ đen quay, vùng này hình thành lên vòng tròn kì dị nằm trong mặt phẳng của xích đạo lỗ đen.[85] Trong cả hai trường hợp, vùng kì dị có thể tích bằng không. Các nhà vật lý cũng chứng minh được rằng vùng kì dị chứa toàn bộ khối lượng của lỗ đen.[86] Do vậy có thể coi vùng này có mật độ vật chất lớn vô hạn.
Cách gọi điểm kì dị hay vòng tròn kì dị hấp dẫn chỉ là tên gọi cho dễ phổ biến. Chúng thường được biểu diễn trên không gian hai hay ba chiều nhằm dễ hình dung bằng trực giác. Còn thực tế vùng kì dị nằm trong không thời gian bốn chiều, và "điểm kì dị" hấp dẫn không phải là điểm hình học Euclid như định nghĩa của nó.[87]
Như phân tích ở trên, chân trời sự kiện là mặt biên trong mêtric mô tả lỗ đen tại r = rS, và dường như một số giá trị vật lý tại mặt này (như thời gian một vật rơi qua biên giới lỗ đen đo bởi người ở xa) có giá trị vô hạn. Nhưng thực chất nó là một mặt định nghĩa bằng thuần túy toán học, xuất hiện do việc lựa chọn hệ tọa độ nhằm miêu tả không thời gian và khi lựa chọn hệ tọa độ khác thì giá trị vô hạn mất đi tại mặt này (còn gọi là kì dị tọa độ).[88] Nhưng đối với vùng kì dị hấp dẫn thì lại khác, các nhà vật lý không thể loại bỏ nó bằng cách chọn một hệ tọa độ phù hợp nào khác. Những kì dị này xuất hiện và là thuộc tính không tránh khỏi của thuyết tương đối tổng quát, với các mêtric miêu tả lỗ đen hay tại thời điểm khai sinh vũ trụ, kì dị Big Bang.[89]
Một vệ tinh kích thước nhỏ đi vào lỗ đen Schwarzschild không thể tránh khỏi chạm vào vùng kì dị một khi nó đã băng qua chân trời sự kiện. Vệ tinh chỉ có thể làm chậm quá trình rơi vào đến gần chân trời bằng cách sử dụng động cơ phản lực, nhưng khi vượt qua nó thì không thể cứu vãn được.[90] Khi vệ tinh chạm đến điểm kì dị, toàn bộ khối lượng của nó sẽ hòa trộn vào mật độ khối lượng vô hạn của kì dị lỗ đen. Trước khi đến trung tâm, vật thể sẽ trải qua tác động của lực thủy triều lên cấu trúc và bị xé tan nát thành những mảnh vụn nhỏ.[91]
Sự xuất hiện không tránh khỏi của các vùng kì dị hấp dẫn trong mêtric không thời gian của thuyết tương đối rộng hàm ý lý thuyết chưa hoàn thiện ở cấp vi mô.[92] Tuy nhiên, sự mất hiệu lực này có thể giải quyết được khi tính tới ảnh hưởng của cơ học lượng tử tại cấp độ vi mô, ở phạm vi mật độ vật chất là rất lớn và 4 tương tác cơ bản giữa các hạt không thể bỏ qua được. Cho tới nay, vẫn chưa có một lý thuyết nhất quán nào kết hợp hiệu quả giữa cơ học lượng tử và hiệu ứng hấp dẫn thành một lý thuyết hoàn chỉnh, mặc dù nhiều nhà vật lý đã đưa ra các mô hình khác về một lý thuyết gọi chung là hấp dẫn lượng tử. Họ cũng hi vọng rằng một khi có được lý thuyết này thì những vùng kì dị sẽ biến mất.[93][94] ngoài ra điểm kì dị của hố đen dẫn vật thể tới một "đường hầm" mà nó sẽ xuyên từ lỗ đen tới lỗ trắng
Mặt cầu photon
Mặt cầu photon là biên giới hạn hình cầu mà những photon có hướng của vectơ vận tốc tiếp tuyến với nó sẽ bị bẫy trong một quỹ đạo tròn là đường tròn lớn của mặt cầu. Đối với lỗ đen không quay, mặt cầu photon có bán kính bằng 1,5 lần bán kính Schwarzschild rS. Trên lý thuyết, photon rơi vào những quỹ đạo này sẽ chuyển động mãi mãi trên đó.[95] Tuy nhiên, về mặt động lực, những quỹ đạo này không ổn định, do vậy bất kỳ một nhiễu loạn nhỏ nào (như các hạt photon tương tác với hạt khác trong quá trình rơi vào lỗ đen) khiến cho hạt hoặc có quỹ đạo hướng thoát ra ngoài hoặc bị hút về phía chân trời sự kiện.[96][97]
Bên trong mặt cầu photon, không thể tồn tại quỹ đạo tròn cho photon. Nếu chiếu tia sáng ra bên ngoài thì nó vẫn có thể thoát khỏi ảnh hưởng của lỗ đen, nhưng nếu chiếu ánh sáng về phía lỗ đen thì ánh sáng sẽ bị nó hấp thụ hoàn toàn. Do vậy nếu một quan sát viên nhận được ánh sáng phát ra từ phía trong mặt cầu photon thì chắc chắn nguồn sáng phải nằm bên trong mặt cầu này và vẫn ở phía ngoài chân trời của lỗ đen.[98]
Những sao đặc khác, như sao neutron, về mặt lý thuyết nếu nó đặc và nhỏ hơn nữa, cũng sẽ có một mặt cầu photon bao quanh.[99] Điều này là do trong thuyết tương đối tổng quát, trường hấp dẫn là biểu hiện sự cong của không thời gian và không phụ thuộc bán kính của vật thể, cho nên bất kỳ một thiên thể nào có bán kính nhỏ hơn 1,5 rS tính theo khối lượng của nó thì sẽ có một mặt cầu photon.[100]
Đối với lỗ đen quay quanh trục miêu tả bởi mêtric Kerr, tồn tại hai quỹ đạo tròn giới hạn của photon đồng phẳng với mặt phẳng xích đạo lỗ đen và những quỹ đạo khác không đồng phẳng, không tròn cho phép photon chuyển động bán ổn định trên đó mặc dù những quỹ đạo này cùng thuộc một mặt cầu-hay quỹ đạo cầu.[96][101] Đối với lỗ đen Kerr, trên mặt phẳng xích đạo, một quỹ đạo tròn tương ứng với các photon chuyển động theo hướng cùng với chiều quay của lỗ đen và nằm gần lỗ đen hơn, còn vòng tròn kia tương ứng với photon chuyển động theo chiều ngược lại và nằm ở xa lỗ đen.[102]
Tuy những quỹ đạo của photon trên mặt cầu này là không ổn định, chúng không có ý nghĩa vật lý do nó chỉ xác định ranh giới cuối cùng mà lỗ đen cho phép tia sáng chuyển động tròn quanh nó. Những mặt cầu và quỹ đạo photon này đóng vai trò quan trọng trong việc hình thành hình ảnh quang học của những đĩa vật chất bồi tụ bao quanh lỗ đen.[95][96]
Vùng sản công

Có một vùng không thời gian bao quanh lỗ đen quay mà khi vật nằm trong vùng này nó không thể đứng im được gọi là mặt cầu sản công (ergosphere). Kết quả này là do ảnh hưởng của hiệu ứng kéo hệ quy chiếu; thuyết tương đối tổng quát tiên đoán rằng một vật quay quanh trục sẽ "kéo" không thời gian lân cận vật đó. Vì vậy bất kỳ vật nào nằm gần khối lượng quay sẽ bắt đầu chuyển động xoay quanh vật trung tâm theo chiều quay của nó. Đối với lỗ đen quay quanh trục, hiệu ứng trở lên rất mạnh gần chân trời sự kiện khiến ngay cả ánh sáng cũng không thể chuyển động ngược với chiều quay của lỗ đen.[103][104]
Vùng sản công của lỗ đen quay giới hạn bởi chân trời sự kiện (ngoài) và bên trong một hình cầu dẹt tiếp xúc với chân trời sự kiện tại hai cực (xem hình). Biên phía ngoài này đôi khi còn gọi là mặt sản công.
Các vật và bức xạ vẫn có thể thoát ra bên ngoài từ trong vùng sản công, chúng thoát ra theo hướng quay của lỗ đen đòi hỏi ít năng lượng hơn so với thoát theo hướng ngược lại. Thông qua cơ chế Penrose, có thể thu năng lượng từ lỗ đen quay bằng cách gửi các vật từ xa bên ngoài vào vùng sản công. Khi vật ở trong vùng này thực hiện một cách nào đó tách nó ra làm hai vật, sao cho một vật rơi vào lỗ đen còn vật kia bắn ra khỏi vùng sản công. Penrose tính toán được khả năng vật bắn ra có năng lượng lớn hơn vật gửi vào. Năng lượng lấy đi này làm lỗ đen quay chậm dần lại theo thời gian, và khi nó ngừng quay thì sẽ không tồn tại vùng sản công nữa.[105][106]
Đi vào bên trong lỗ đen và du hành thời gian
- Xem thêm mô phỏng đi vào lỗ đen tại trang jila.colorado.edu
Mọi thứ rơi qua chân trời lỗ đen vào vùng kì dị đều bị phá hủy hoàn toàn. Nhưng giả sử có nhà du hành vũ trụ mạo hiểm bắt đầu tiến gần thăm dò một lỗ đen siêu khối lượng bằng con tàu của mình. Lúc ở xa, người đó và con tàu ở trong trạng thái không trọng lượng vì lực hấp dẫn khá yếu, cơ thể anh ta cũng không cảm thấy có lực kéo nào.[107][108]
Đối với lỗ đen càng lớn, lực thủy triều gần chân trời sự kiện càng yếu hơn so với lỗ đen nhỏ hơn. Điều này cho phép con tàu có khả năng tiếp cận biên giới lỗ đen. Giả sử nhà du hành ngồi lái với chân anh ta hướng về lỗ đen. Càng gần biên giới, nhà du hành cảm thấy rõ rệt lực thủy triều tác động lên phía chân mạnh hơn so với phần đầu. Giả sử con tàu và nhà du hành chịu được sức ép và kéo; và băng qua chân trời sự kiện lỗ đen. Trong con tàu, nơi hệ tọa độ là cục bộ, anh ta sẽ không biết khi nào hay cảm giác gì lúc con tàu băng qua mặt biên này (ngoại trừ lực thuỷ triều).[107][108]
- Trong lúc đi vào, nếu anh ta nhìn ngược ra phía ngoài vũ trụ, nhà du hành sẽ thấy các ngôi sao nằm lệch khỏi vị trí của chúng, càng vào sâu thì các ngôi sao càng sáng hơn và nằm gần nhau hơn. Điều này là do lỗ đen làm uốn cong không thời gian và hiệu ứng dịch chuyển đỏ do hấp dẫn làm bước sóng tia sáng phát ra từ các ngôi sao bị hút về lỗ đen dịch chuyển về phía tím nhiều hơn. Khi đã băng qua chân trời, chỉ hết thời gian hữu hạn đo ở trong con tàu, anh ta cùng con tàu sẽ không tránh khỏi bị phá hủy bởi hiệu ứng thủy triều cực mạnh và hòa vào vùng kì dị của lỗ đen.[107][108]
- Còn đối với người ở ngoài xa lỗ đen, thông qua tín hiệu con tàu phát ra (hay hình ảnh của nó), họ sẽ thấy con tàu rơi chậm dần về phía chân trời sự kiện. Tín hiệu nhận được sẽ chuyển dần từ bước sóng ngắn sang bước sóng dài hơn hay dịch chuyển đỏ hơn. Và dường như phải đợi rất lâu (gần như lâu vô hạn, đo bởi đồng hồ nằm rất xa lỗ đen) để thấy con tàu rơi qua biên giới lỗ đen. Người ở xa nhận được tín hiệu có bước sóng càng lúc càng dài, đến khi thiết bị của họ không còn khả năng thu được bước sóng dài đó nữa thì coi như hình ảnh và tín hiệu con tàu đã biến mất.[107][108][109]
Trong trường hợp của lỗ đen tích điện (Reissner–Nordström) hay lỗ đen quay quanh trục (Kerr), khi rơi vào chúng, về lý thuyết có thể tránh được vùng kì dị hấp dẫn. Bằng cách mở rộng miêu tả toán học những nghiệm này lên mức tổng quát nhất có thể, các nhà vật lý nhận thấy có khả năng một người đi vào những lỗ đen này sẽ thoát sang một vùng không thời gian khác, và lúc này lỗ đen trở thành một chiếc cổng nối hay là lỗ sâu đục.[110] Tuy nhiên xác suất để du hành sang một vũ trụ khác là rất thấp do chỉ cần một nhiễu loạn nhỏ trong lỗ đen sẽ ngay lập tức phá hủy chiếc cầu nối này và thay vào đó người đó sẽ rơi trở lại vùng kì dị hấp dẫn.[111] Cũng có một khả năng cho phép du hành theo những cung đóng kiểu thời gian (hay là quay ngược trở lại quá khứ của chính nhà du hành) xung quanh vòng kì dị của lỗ đen Kerr, nhưng nó lại dẫn đến những vấn đề nguyên nhân - kết quả như nghịch lý ông nội (người cháu có khả năng trở về quá khứ và gặp lại ông nội của mình).[112] Các nhà lý thuyết cho rằng không thể tồn tại những khả năng kì lạ này một khi tính đến những hiệu ứng lượng tử cho lỗ đen mang điện tích hoặc quay quanh trục.[113]
Nếu như nhà du hành thay vì đi thẳng vào lỗ đen, anh ta lái con tàu quay quanh nó rất nhiều vòng thì hiệu ứng giãn thời gian do hấp dẫn làm cho thời gian trôi trong con tàu chậm hơn so với thời gian đo bởi đồng hồ ở rất xa lỗ đen. Sau khi quay đủ nhiều vòng, con tàu rời lỗ đen và trở về nơi xuất phát. Lúc này nhà du hành có độ tuổi trẻ hơn nhiều so với những người tại đây, và coi như anh ta đã du hành đến tương lai của chính mình.[114]
Sự hình thành và tiến hóa
Các hố đen có thể hình thành khi một ngôi sao khổng lồ bùng phát ra nhiên liệu hạt nhân và sụp đổ dưới trọng lực riêng của nó. Nếu ngôi sao đủ lớn không có lực nào có thể chống lại lực hấp dẫn ngày càng tăng, và nó sẽ sụp đổ đến một điểm mật độ vô hạn. Trước khi đạt đến giai đoạn này, trong phạm vi bán kính nhất định (chân trời sự kiện) bản thân ánh sáng trở nên bị mắc kẹt và vật thể trở nên vô hình.[4]
Với những tính chất kỳ lạ của lỗ đen như đã nêu, một câu hỏi tự nhiên xuất hiện là những thiên thể kì quái này có tồn tại trong tự nhiên hay chúng chỉ là những nghiệm toán học trong phương trình Einstein. Năm 1939, trong một bài báo của Einstein, ông nghĩ là lỗ đen không hình thành trong vũ trụ, với lập luận rằng mô men động lượng quay của các hạt trong quá trình suy sụp giúp ổn định chúng tại một số bán kính nhất định.[115][116][117] Nhưng chỉ vài tháng sau, Oppenheimer và cộng sự lần đầu tiên chỉ ra khả năng lỗ đen hình thành như thế nào bằng thuyết tương đối tổng quát.[117] Khi Schwarzschild tìm ra nghiệm của ông, ban đầu các nhà vật lý nghĩ rằng lỗ đen có thể tồn tại tuân theo các định luật vật lý. Sau đó, trong nhiều năm Einstein và cộng đồng vật lý lại nghĩ nó không tồn tại, chỉ có một số người mới nghiêm túc quan tâm đến câu hỏi về sự tồn tại của thực thể này[118] và cho đến cuối thập niên 1950, họ đã chứng minh được không thể có gì cản trở những ngôi sao khối lượng lớn suy sụp trở thành lỗ đen bao bởi chân trời sự kiện.[119]
Khi chân trời sự kiện hình thành trong giai đoạn suy sụp, Penrose chứng minh được là vùng kì dị hấp dẫn cũng phải hình thành ở bên trong nó.[43] Ngay sau đó, Hawking chỉ ra rằng các mô hình miêu tả vũ trụ về thời điểm Vụ Nổ Lớn cũng xuất hiện những kì dị hấp dẫn mà không cần đến dạng vật chất lạ nào (xem định lý kì dị hấp dẫn Penrose-Hawking). Mêtric Kerr, định lý "không có tóc" các định luật của nhiệt động học lỗ đen cho thấy các tính chất vật lý của lỗ đen là đơn giản và có thể nắm bắt được, lúc này các thiên thể đặc từ những đối tượng lý thuyết trở thành ngành nghiên cứu của thiên văn vật lý.[120] Quá trình cơ bản hình thành lỗ đen đó là sự suy sụp hấp dẫn của những thiên thể khối lượng lớn như các ngôi sao già..., nhưng cũng có những quá trình khác dẫn đến hình thành lỗ đen. Thông qua quan sát tại bước sóng vô tuyến, hồng ngoại và tia X...trên mặt đất hay từ các đài quan sát vệ tinh đã chứng tỏ là lỗ đen quả thực tồn tại trong vũ trụ.[6]
Suy sụp hấp dẫn
Giai đoạn suy sụp hấp dẫn xuất hiện khi áp suất trong lòng vật thể không còn đủ lớn để chống lại lực hút hấp dẫn của chính nó. Đối với ngôi sao, quá trình này xuất hiện hoặc là do nó có quá ít "nhiên liệu" còn lại để duy trì nhiệt độ thông qua các phản ứng tổng hợp hạt nhân sao, hoặc bởi vì ngôi sao nhận thêm vật chất từ môi trường hoặc từ sao đồng hành khiến cho lực hấp dẫn của nó lớn hơn áp suất trong lòng ngôi sao. Trong cả hai trường hợp, áp suất không đủ lớn để ngăn cản sự suy sụp hấp dẫn dưới chính khối lượng của nó.[121] Quá trình suy sụp có thể dừng lại bởi "áp suất lượng tử" của các thành phần hạt vật chất trong ngôi sao, hình thành lên dạng vật chất với mật độ rất lớn trong nó. Kết quả này mang lại có một số kiểu sao đặc khác nhau. Kiểu sao đặc hình thành phụ thuộc vào khối lượng vật chất còn lại sao khi những lớp bên ngoài đã bị thổi bay đi, như từ vụ nổ siêu tân tinh hoặc bởi gió sao thổi vật chất vào môi trường liên sao tạo nên tinh vân hành tinh. Do vậy khối lượng tàn dư thường nhỏ hơn rất nhiều khối lượng của sao gốc—ví dụ những thiên thể tàn dư có khối lượng trên 5 lần khối lượng Mặt Trời hình thành từ những ngôi sao ban đầu có khối lượng trên 20 lần khối lượng Mặt Trời trước khi nó suy sụp hấp dẫn.[121]
Nếu khối lượng tàn dư vượt hơn 3–4 khối lượng Mặt Trời (giới hạn Tolman–Oppenheimer–Volkoff[25])—do bởi ngôi sao gốc có khối lượng rất lớn hoặc do bởi thiên thể tàn dư tích tụ thêm vật chất thông qua đĩa bồi tụ—thì ngay cả áp suất lượng tử của các hạt neutron (tuân theo nguyên lý loại trừ Pauli) là không đủ lớn để ngăn cản lực hấp dẫn để tiến tới suy sụp hấp dẫn. Không một cơ chế nào khác (ngoại trừ khả năng áp suất gây bởi vật chất quark, xem sao quark) đủ mạnh để ngăn cản sự nổ vào bên trong và thiên thể đặc không thể tránh khỏi hình thành lên lỗ đen.[121]
Các nhà vật lý lý thuyết cho rằng các lỗ đen khối lượng sao hình thành từ quá trình suy sụp hấp dẫn của các ngôi sao gốc khối lượng lớn. Sự hình thành sao trong lúc vũ trụ còn sơ khai có thể dẫn đến những ngôi sao có khối lượng rất lớn, với giai đoạn cuối đời của chúng tạo ra những lỗ đen khối lượng cỡ ~102 khối lượng Mặt Trời. Những lỗ đen này có thể là mầm hình thành lên lỗ đen siêu khối lượng thường tìm thấy tại trung tâm của các thiên hà.[122]
Trong khi đa số năng lượng giải phóng trong quá trình suy sụp hấp dẫn phát ra rất nhanh, một người ở xa bên ngoài không thực sự nhìn thấy quá trình này kết thúc. Ngay cả khi nó chỉ diễn ra trong một thời gian hữu hạn đối với hệ quy chiếu của vật chất đang rơi suy sụp, quan sát viên ở xa sẽ thấy vật chất rơi về trung tâm chậm dần và dừng lại ngay trước chân trời sự kiện, do hiệu ứng "giãn thời gian do hấp dẫn". Ánh sáng phát ra từ vật chất co sụp càng mất thời gian lâu hơn để đến được vùng bên ngoài, với ánh sáng phát ra ngay trước khi vật chất băng qua chân trời sự kiện mất khoảng thời gian gần vô hạn để tới được quan sát viên. Do vậy, người này sẽ không thể nhìn thấy hình thành chân trời sự kiện của lỗ đen. Vật chất suy sụp theo thời gian trở lên mờ hơn và bước sóng ánh sáng phát ra dịch chuyển về phía đỏ nhiều hơn và cuối cùng tàn lụi đi, không còn thứ ánh sáng nào nữa.[123]
Lỗ đen nguyên thủy sau Vụ Nổ Lớn
Suy sụp hấp dẫn đòi hỏi mật độ vật chất lớn. Trong kỷ nguyên hiện tại của vũ trụ những mật độ cao này chỉ tồn tại trong các sao, nhưng vào lúc vũ trụ mới hình thành sau Vụ Nổ Lớn mật độ vật chất lúc đó rất cao, với khả năng cho phép hình thành các lỗ đen nguyên thủy. Nếu chỉ có mật độ cao không thôi thì chưa đủ để cho phép hình thành lỗ đen bởi vì sự phân bố khối lượng đồng đều không khiến vật chất tích tụ lại với nhau. Để những lỗ đen nguyên thủy hình thành trong môi trường đậm đặc này, ban đầu phải có sự thăng giáng mật độ cho phép vật chất tích tụ lại với nhau nhờ lực hấp dẫn. Các mô hình khác nhau về thời kỳ sơ khai của vũ trụ cho những tiên đoán khác nhau về mức độ thăng giáng này. Một số mô hình tiên đoán các lỗ đen nguyên thủy sẽ hình thành, từ cấp độ khối lượng Planck cho đến hàng trăm lần khối lượng Mặt Trời.[124] Lỗ đen nguyên thủy có thể tham gia vào quá trình hình thành lên lỗ đen khối lượng trung gian và lỗ đen siêu khối lượng.
Hình thành từ các hạt va chạm năng lượng cao

Ngoài quá trình suy sụp hấp dẫn hình thành lên lỗ đen, về nguyên lý thì những va chạm hạt năng lượng cao trong các máy gia tốc cũng có thể hình thành lỗ đen khi đạt mật độ cho phép.[125] Cho đến 2013, chưa một sự kiện nào được xác nhận, trực tiếp hay gián tiếp, một lỗ đen siêu nhỏ hình thành trong các máy gia tốc hạt.[126] Về mặt lý thuyết, giới hạn khối lượng cho phép hình thành lỗ đen siêu nhỏ nằm trong khoảng khối lượng Planck (mP = √ħc/G ≈ 1,2 × 1019 ≈ 2,2 × 10−8 kg), nơi các hiệu ứng lượng tử có ảnh hưởng đáng kể.[127] Giới hạn này cho thấy trong mức hoạt động hiện nay của một số máy gia tốc thì không có khả năng sinh ra các lỗ đen siêu nhỏ. Mặt khác, một số lý thuyết về hấp dẫn lượng tử cho kết quả khối lượng Planck có thể còn có giá trị thấp hơn: có mô hình "thế giới brane" tính ra giá trị này bằng 1 TeV/c2.[128][129] Điều này cho phép các lỗ đen vi mô có thể sinh ra trong tích tắc tại những va chạm năng lượng cao của LHC tại CERN, hoặc chúng có thể sinh ra từ những tia vũ trụ năng lượng cao đi vào bầu khí quyển Trái Đất.[126] Mặc dù các lý thuyết là rất gợi mở, nhưng một số nhà vật lý không ủng hộ cho khả năng xuất hiện các lỗ đen siêu nhỏ trong các máy gia tốc nhân tạo.[130] Ngay cả khi những lỗ đen này hình thành, theo lý thuyết chúng sẽ nhanh chóng bốc hơi với khoảng thời gian 10−25 giây, và không gây ảnh hưởng đến Trái Đất.[126] Sự hình thành lỗ đen vi mô cũng liên quan tới phỏng đoán vòng về chu vi giới hạn của vật thể sau quá trình va chạm hoặc suy sụp.[62][129]
Phát triển và sáp nhập


Trong thời gian tồn tại của lỗ đen, nó có thể tăng thêm khối lượng bằng quá trình hút vật chất từ không gian xung quanh vào. Nó sẽ liên tục hấp thụ khí và bụi liên sao từ môi trường xung quanh và cả bức xạ nền vi sóng vũ trụ. Quá trình hấp thụ khối lượng là một trong những quá trình cơ bản hình thành lên lỗ đen siêu khối lượng.[122] Và có thể quá trình này cũng áp dụng cho các lỗ đen khối lượng trung gian nằm ở các cụm sao cầu.[131]
Một cơ chế khác đó là lỗ đen sáp nhập với các thiên thể khác như sao hay chính lỗ đen. Quá trình này đặc biệt quan trọng vì nó mang lại khả năng giải thích hợp lý tại sao lại có những lỗ đen khổng lồ, mà chúng hình thành từ việc sáp nhập nhiều lỗ đen nhỏ hơn.[122] Các lỗ đen khối lượng khổng lồ nằm tại tâm mỗi thiên hà có thể sáp nhập với nhau trong giai đoạn hai thiên hà va chạm và sáp nhập, và quá trình này có thể xảy ra đối với lỗ đen khối lượng trung gian, như Omega Centauri.[132][133]
Quá trình thu hút vật chất về phía lỗ đen sẽ hình thành lên một đĩa sáng bồi tụ chứa vật chất trạng thái plasma nóng hàng triệu độ, và vùng này phát ra nguồn tia X rất mạnh.[134][135] Chớp tia gamma thu được từ các đài quan sát vệ tinh phát ra từ những nguồn ở rất xa cũng có thể giải thích từ quá trình sáp nhập hai sao đặc hoặc bởi lỗ đen hút các sao đặc khác. Thông qua nguồn tia X mà các nhà thiên văn có thể nhận biết ra sự tồn tại của lỗ đen.[11]
Hai lỗ đen quay quanh nhau sẽ phát ra sóng hấp dẫn mang năng lượng của hệ đi. Do mất năng lượng, chúng sẽ có quỹ đạo càng gần nhau hơn, cuối cùng khi hòa nhập lại sẽ hình thành một lỗ đen khối lượng lớn hơn và quay rất nhanh quay trục. Lỗ đen mới có thể bị đẩy ra khỏi vùng của hai lỗ đen ban đầu với vận tốc cỡ 400 km/s, và thậm chí sau thời gian dài nó có thể thoát khỏi thiên hà ban đầu.[136]
Bốc hơi
Năm 1974, Hawking chứng minh rằng lỗ đen không hoàn toàn đen mà có phát ra một lượng nhỏ bức xạ nhiệt;[46] một hiệu ứng mà ngày nay gọi là bức xạ Hawking. Bằng cách áp dụng lý thuyết trường lượng tử cho một lỗ đen đứng yên trong không thời gian, ông xác định được nó sẽ phát ra các hạt trong phổ bức xạ vật đen tuyệt đối. Từ sau bài báo của Hawking, nhiều người đã xác nhận kết quả theo nhiều cách tiếp cận khác nhau.[137] Nếu lý thuyết của Hawking về lỗ đen bức xạ là đúng, thì các lỗ đen sẽ giảm dần khối lượng và bốc hơi sau một thời gian bởi vì chúng mất khối lượng thông qua năng lượng của các hạt phát ra.[46] Nhiệt độ của phổ bức xạ (nhiệt độ Hawking) tỷ lệ với giá trị hấp dẫn bề mặt của lỗ đen, mà đối với lỗ đen Schwarzschild, nhiệt độ tỷ lệ nghịch với khối lượng của nó. Do vậy, các lỗ đen khối lượng lớn phát ra ít bức xạ hơn so với lỗ đen khối lượng nhỏ hơn.[138]
Giả sử một lỗ đen có khối lượng bằng khối lượng Mặt Trời thì nó có nhiệt độ Hawking bằng 100 nanokelvin. Giá trị này nhỏ hơn hẳn nhiệt độ 2,7 K của bức xạ nền vi sóng vũ trụ. Do đó lỗ đen khối lượng sao hay lớn hơn sẽ nhận thêm khối lượng từ bức xạ nền vũ trụ so với lượng nhỏ bức xạ Hawking chúng phát ra, và vì vậy chúng lớn lên thay vì nhỏ dần đi. Để có nhiệt độ Hawking lớn hơn 2,7 K (và cho phép bốc hơi), lỗ đen phải có khối lượng nhỏ hơn khối lượng Mặt Trăng. Những lỗ đen này chỉ có đường kính bé hơn 1/10 của milimét.[139]
Lỗ đen càng nhỏ thì hiệu ứng bức xạ càng mạnh. Một lỗ đen có khối lượng bằng người bình thường sẽ ngay lập tức bốc hơi. Lỗ đen khối lượng bằng chiếc ô tô có đường kính khoảng 10−24 m bốc hơi xấp xỉ sau 1 nano giây, lúc đó nó sẽ phát sáng gấp 200 lần độ sáng Mặt Trời. Lỗ đen nhỏ hơn có thời gian bốc hơi ngắn hơn nữa; lỗ đen khối lượng 1 TeV/c2 chỉ cần ít hơn 10−88 giây để biến mất. Đối với những lỗ đen vi mô, các nhà khoa học kỳ vọng hiệu ứng hấp dẫn lượng tử trở lên đáng kể—mặc dù những phát triển hiện tại không cho thấy điều này[140]—và trên lý thuyết cho phép những lỗ đen vi mô có thể tồn tại ổn định.[141] Tuy lỗ đen có thể bốc hơi theo lý thuyết, nhưng nó không thể tách thành hai lỗ đen nhỏ hơn, lỗ đen chỉ có thể sáp nhập với nhau.[142]
Quan sát
Lỗi Lua trong Mô_đun:Multiple_image tại dòng 301: attempt to concatenate a boolean value.
Theo tính chất của lỗ đen, nó không trực tiếp phát ra bất kỳ một tín hiệu nào ngoài giả thiết bức xạ Hawking; do trong phạm vi thiên văn vật lý bức xạ Hawking là rất yếu, cho nên không thể quan sát thấy bức xạ này từ Trái Đất. Trường hợp ngoại lệ cho bức xạ Hawking đó là giai đoạn cuối cùng của những lỗ đen nguyên thủy bốc hơi phát ra nó; mặc dù chưa tìm kiếm thành công và điều này đặt ra giới hạn cho khả năng tồn tại bức xạ này từ những lỗ đen nguyên thủy.[143] Kính thiên văn không gian tia gamma Fermi của NASA phóng lên 2008 với một trong những mục đích của nó là thu thập những tín hiệu này.[144]
Quan sát thiên văn vật lý về lỗ đen phải dựa trên những quan sát gián tiếp. Sự tồn tại của lỗ đen có thể suy ra từ các ảnh hưởng hấp dẫn của nó với môi trường xung quanh. Một trong số những cuộc khảo sát đó là dự án "Kính thiên văn Chân trời sự kiện" hợp tác giữa các tổ chức quốc tế đang nỗ lực lần đầu tiên quan sát trực tiếp được vùng bao quanh chân trời sự kiện của lỗ đen.[145]
Đo sóng hấp dẫn từ hai hố đen sáp nhập
Ngày 14 tháng 9 năm 2015, hai Trạm quan sát sóng hấp dẫn bằng giao thoa kế laser LIGO đã đo được trực tiếp sóng hấp dẫn.[14][146] Tín hiệu thu được khớp với dự đoán bằng lý thuyết và mô phỏng máy tính cho sóng hấp dẫn phát ra từ sự sáp nhập của hai lỗ đen: một hố đen có khối lượng 36 lần khối lượng Mặt Trời, và hố đen kia có khối lượng 29 lần khối lượng Mặt Trời (đo trong hệ quy chiếu gắn với hệ).[14][147] Quan sát này cung cấp chứng cứ cụ thể nhất cho sự tồn tại của lỗ đen cho tới ngày nay. Ví dụ, tín hiệu sóng hấp dẫn gợi ra rằng khoảng cách giữa hai vật thể trước va chạm chỉ bằng 350 km (hay gần bằng 4 lần bán kính Schwarzschild tương ứng với khối lượng của vật thể). Hai vật thể này từ đó phải cực kỳ đặc, để lại cách giải thích hợp lý nhất chúng phải thực sự là các hố đen.[14]
Quan trọng hơn, tín hiệu đo được bởi LIGO cũng thu được giai đoạn sau sáp nhập (ringdown), tín hiệu phát ra từ vật thể đặc mới hình thành nhanh chóng tắt tới trạng thái dừng (nếu không phải là lỗ đen, tín hiệu sau va chạm sẽ thăng giáng rất lớn bởi sự kiện va chạm của hai vật thể có khối lượng cỡ như thế). Có thể nói, tín hiệu dao động tắt lịm nhanh chóng sau va chạm là cách trực tiếp nhất để khẳng định đó là một lỗ đen.[148] Từ dữ liệu của LIGO, có thể phân tích ra tần số và thời gian tắt của giai đoạn ringdown này. Từ tần số và tốc độ biến thiên tần số đo được ở giai đoạn này, các nhà vật lý tính ra được khối lượng và mô men động lượng của vật thể cuối cùng, mà giá trí tính được khớp một cách độc lập với mô phỏng bằng siêu máy tính của sự kiện va chạm và sáp nhập.[149] Tần số và khoảng thời gian biến thiên của mốt điển hình được xác định bởi hình học của mặt cầu photon. Vì vậy, quan sát mốt này xác nhận sự có mặt của mặt cầu photon, tuy nhiên nó không thể ngoại trừ khả năng kỳ lạ khác thay cho hố đen mà vật thể đủ đặc để có một mặt cầu photon.[148]
Quan sát này cũng lần đầu tiên cung cấp bằng chứng thực nghiệm về sự tồn tại của cặp lỗ đen khối lượng sao. Hơn nữa, đây là chứng cứ thực tế đầu tiên về những lỗ đen có khối lượng lớn hơn 25 lần khối lượng Mặt Trời.[150]
Đĩa bồi tụ vật chất
Theo định luật bảo toàn mô men động lượng, khí và bụi rơi vào "giếng hấp dẫn" của vật thể lớn sẽ hình thành lên cấu trúc dạng đĩa chứa plasma bao quanh vật thể. Plasma tiếp xúc ma sát với nhau do mô men động lượng truyền từ bên ngoài vào, dẫn đến giải phóng năng lượng dưới dạng bức xạ điện từ và làm tăng nhiệt độ của đĩa bồi tụ lên hàng triệu độ.[134][151] Nguồn bức xạ sóng ngắn phát ra từ vùng bồi tụ của sao lùn trắng, sao neutron hoặc lỗ đen cho phép các kính thiên văn phát hiện ra nguồn này. Quá trình bồi tụ là một trong những quá trình sản sinh năng lượng hiệu quả nhất từng được biết; tới khoảng 40% khối lượng nghỉ của vật chất trong đĩa bị biến đổi thành dạng năng lượng bức xạ.[151] (ở các phản ứng tổng hợp hạt nhân chỉ khoảng 0,7% khối lượng nghỉ giải phóng dưới dạng năng lượng bức xạ.) Trong nhiều trường hợp, đĩa bồi tụ thường đi kèm với chùm tia tương đối tính phát ra dọc hai cực của thiên thể đặc, mang theo năng lượng với các hạt có vận tốc rất lớn. Các nhà vật lý vẫn chưa hiểu thực sự cơ chế hình thành những tia này.
Một trong những cơ chế lý giải hình thành các tia phát ra từ hai cực lỗ đen đó là do sự kết hợp giữa vùng sản công và từ trường lỗ đen tác động lên các hạt vật chất rơi về lỗ đen, một số rơi qua chân trời sự kiện, một số vật chất bắn ngược ra bên ngoài tạo nên hai tia đối cực.[152]
Nhiều hiện tượng năng lượng cao trong vũ trụ có nguồn gốc từ đĩa bồi tụ vật chất quanh lỗ đen. Đặc biệt, nhân thiên hà hoạt động hoặc quasar được cho là do bức xạ phát ra từ đĩa vật chất bao quanh lỗ đen siêu khối lượng.[64] Tương tự, nguồn tia X trong những hệ sao đôi xuất phát từ một trong hai thiên thể là sao đặc với đĩa bồi tụ.[64] Một số nguồn tia X siêu sáng có thể là các vùng bồi tụ quanh lỗ đen khối lượng trung gian.[153] Do hiệu ứng lực thủy triều, nhiệt độ trong các đĩa bồi tụ của lỗ đen khối lượng sao lớn hơn nhiệt độ của đĩa bồi tụ ở lỗ đen siêu khối lượng.[154] Phổ bức xạ mạnh nhất phát ra từ vùng bồi tụ của lỗ đen siêu khổng lồ là miền tử ngoại, trong khi đối với các lỗ đen khối lượng sao là miền tia X. Tuy vậy, độ sáng phát ra từ vùng lân cận quanh lỗ đen siêu khối lượng lại sáng hơn hàng trăm nghìn tỷ lần Mặt Trời, trong khi đối với lỗ đen khối lượng sao là hàng triệu lần độ sáng Mặt Trời.[154]
Nguồn tia X trong hệ sao đôi

Nguồn tia X trong hệ sao đôi thuộc về hệ thống sao đôi với năng lượng phát ra chủ yếu trong phổ của tia X. Đa phần những nguồn này là do một trong những sao đặc bồi tụ vật chất lấy từ sao đồng hành trong hệ. Sự có mặt của những ngôi sao đồng hành trong các hệ này cho phép các nhà thiên văn có cơ hội nghiên cứu chi tiết thiên thể đặc trung tâm và có thể là lỗ đen.[154]
Nếu tín hiệu phát ra thuộc về thiên thể đặc (bỏ qua tín hiệu thuộc về vùng bồi tụ), thì thiên thể này không thể là lỗ đen. Tuy nhiên, nếu thiên thể đặc không phát ra tín hiệu nào, thì vẫn chưa thể loại trừ khả năng nó là một sao neutron. Bằng cách nghiên cứu sao đồng hành cho phép đo và tính ra các tham số quỹ đạo của hệ, từ đó các nhà thiên văn có thể tính ra khối lượng của thiên thể đặc. Nếu giá trị này lớn hơn giới hạn Tolman–Oppenheimer–Volkoff (khối lượng lớn nhất mà một sao neutron có thể đạt được sau giai đoạn suy sụp hấp dẫn) thì vật thể đặc không thể là sao neutron mà xác suất cao đó là một lỗ đen.[64]
Khả năng thuyết phục mạnh đầu tiên về một lỗ đen tồn tại, Cygnus X-1, do nhà thiên văn Charles Thomas Bolton,[155] Louise Webster và Paul Murdin[156] phát hiện nhờ vào phương pháp này năm 1972.[157][158] Tuy nhiên, ban đầu có những sai số trong kết quả đo và khối lượng của sao đồng hành có giá trị tương đối lớn.[154] Hiện tại, nhiều ứng cử viên là lỗ đen được tìm thấy trong lớp các hệ sao đôi tia X gọi là nguồn chuyển tiếp tia X năng lượng thấp (soft X-ray transients).[64] Trong lớp này, khối lượng của sao đồng hành khá thấp cho phép ước lượng chính xác hơn khối lượng của lỗ đen. Hơn nữa, mỗi lần tia X phát ra từ những hệ này chỉ có thời gian trong vài tháng với khoảng chu kỳ 10–50 năm. Trong thời gian nguồn tia X ngừng phát hoặc yếu, vùng bồi tụ trở lên rất mờ cho phép thực hiện quan sát chi tiết về sao đồng hành. Một trong những hệ như thế là V404 Cyg.
Thời gian ngừng hoạt động
Sự mờ nhạt của đĩa trong thời gian nó ngừng hoạt động có thể là nguyên nhân luồng vật chất ở vào giai đoạn lạnh đi (ADAF). Trong giai đoạn này, đa phần năng lượng của plasma trong đĩa bị giam giữ dọc theo luồng hạt hơn là phát ra theo mọi phía. Nếu mô hình này là đúng, thì đây là một trong những bằng chứng thực nghiệm chứng tỏ tồn tại chân trời sự kiện.[159] Bởi vì, nếu vật thể ở trung tâm của đĩa bồi tụ có bề mặt rắn, nó sẽ phát ra một lượng lớn bức xạ năng lượng cao khi khí và plasma va đập xuống bề mặt của nó, một hiệu ứng đã được quan sát ở sao neutron trong cùng trạng thái này.[151] (xem mô phỏng nguồn tia X của hai lỗ đen GRS 1915 và IGR J17091 về khoảng thời gian ngừng phát tia X.)
Dao động gần tuần hoàn
Bức xạ tia X từ đĩa bồi tụ đôi khi lặp lại theo những khoảng gần đều đặn trong phổ thu được. Những tín hiệu này được gọi là dao động gần tuần hoàn và khả năng chúng phát ra từ vùng trong cùng của đĩa bồi tụ (nơi quỹ đạo tròn ổn định của hạt có bán kính nhỏ nhất - quỹ đạo này trong lỗ đen Schwarzschild có giá trị 3rS, lớn hơn quỹ đạo của photon[160]). Những tần số tia X này có liên hệ với khối lượng của thiên thể đặc và là phương pháp khác để xác định khối lượng của lỗ đen.[161] (xem mô phỏng nguồn tia X của hai lỗ đen GRS 1915 và IGR J17091 về sự lặp lại gần tuần hoàn của cường độ tia X.)
Nhân thiên hà
Các nhà thiên văn học sử dụng thuật ngữ "thiên hà hoạt động" để miêu tả các thiên hà với những đặc trưng khác lạ, như vạch quang phổ phát xạ bất thường hay bức xạ vô tuyến mạnh. Những nghiên cứu lý thuyết và quan sát cho thấy sự hoạt động trong các nhân thiên hà có thể giải thích bởi tồn tại các lỗ đen siêu khối lượng. Các mô hình về nhân thiên hà hoạt động (AGN) bao gồm một lỗ đen trung tâm với khối lượng vài triệu đến hàng tỷ lần khối lượng Mặt Trời; một đĩa bồi tụ gồm khí và bụi liên sao bao quanh; và hai luồng tia tương đối tính phóng ra gần vuông góc với mặt phẳng đĩa.[162][163]
Các nhà thiên văn cho rằng các lỗ đen khổng lồ sẽ được tìm thấy tại trung tâm thiên hà hoạt động, mặc dù chỉ một số nhân thiên hà đã được nghiên cứu kỹ lưỡng nhằm phát hiện và đo đạc khối lượng của lỗ đen nằm ở trung tâm. Những thiên hà nổi bật với khả năng chứa lỗ đen siêu khối lượng bao gồm thiên hà Andromeda, M32, M87, NGC 3115, NGC 3377, NGC 4258, NGC 4889, NGC 1277, OJ 287, APM08279+5255 và thiên hà Sombrero.[164]
Ngày nay, phần lớn cộng đồng thiên văn học đều công nhận rằng không chỉ tại các thiên hà hoạt động, mà đa số các thiên hà lớn đều chứa ít nhất một lỗ đen siêu khối lượng.[165] Có một mối liên hệ trong thực nghiệm giữa khối lượng của lỗ đen và vận tốc quay của chỗ phình thiên hà chứa nó, hay liên hệ M-sigma, cho biết mối liên hệ giữa sự hình thành của lỗ đen cũng như khối lượng của chúng với quá trình tiến hóa thiên hà.[166]
Chuyển động riêng của các ngôi sao quanh Sagittarius A*
Hiện tại, có những bằng chứng thuyết phục về một lỗ đen khổng lồ tại trung tâm của Ngân Hà, thông qua việc nghiên cứu chuyển động riêng của các ngôi sao quanh vùng này.[12] Từ năm 1995, các nhà thiên văn thực hiện theo dõi chuyển động của 90 sao trong một vùng gọi là Sagittarius A*. Bằng cách làm khớp số liệu quan sát với các tham số của quỹ đạo Kepler, họ kết luận vào năm 1998 rằng phải có vật thể khối lượng 2,6 x 106 M![]() nằm trong vùng bán kính 0,02 ly.[168] Sau khi một ngôi sao gọi là S2 hoàn thành xong một vòng quỹ đạo, những dữ liệu thu được cho phép các nhà khoa học ước tính khối lượng và phạm vi chính xác hơn của vật trung tâm ở Sagittarius A*. Họ đã tính ra có một thiên thể khối lượng 4,3 x 106 M
nằm trong vùng bán kính 0,02 ly.[168] Sau khi một ngôi sao gọi là S2 hoàn thành xong một vòng quỹ đạo, những dữ liệu thu được cho phép các nhà khoa học ước tính khối lượng và phạm vi chính xác hơn của vật trung tâm ở Sagittarius A*. Họ đã tính ra có một thiên thể khối lượng 4,3 x 106 M![]() nằm trong bán kính nhỏ hơn 0,002 ly.[12] Mặc dù bán kính này vẫn lớn hơn 3.000 lần bán kính Schwarzschild của lỗ đen cùng khối lượng, nhưng theo thuyết tương đối tổng quát, những thiên thể có khối lượng lớn như vậy phải là một lỗ đen, và "không có một cụm sao nào có thể tập trung khối lượng lớn như vậy trong một vùng rất nhỏ".[168] (khoảng cách từ Mặt Trời đến sao gần nhất Proxima Centauri là 4,24 ly.)
nằm trong bán kính nhỏ hơn 0,002 ly.[12] Mặc dù bán kính này vẫn lớn hơn 3.000 lần bán kính Schwarzschild của lỗ đen cùng khối lượng, nhưng theo thuyết tương đối tổng quát, những thiên thể có khối lượng lớn như vậy phải là một lỗ đen, và "không có một cụm sao nào có thể tập trung khối lượng lớn như vậy trong một vùng rất nhỏ".[168] (khoảng cách từ Mặt Trời đến sao gần nhất Proxima Centauri là 4,24 ly.)
Chớp tia gamma
Chớp tia gamma là một trong những nguồn tia gamma mang năng lượng lớn nhất trong vũ trụ phát ra từ các thiên hà ở xa.[169] Cơ chế giải thích cho những nguồn này có thể bắt nguồn từ sự sáp nhập của hai sao neutron, bởi lỗ đen hút sao đặc đồng hành hay bởi vùng bồi tụ quanh lỗ đen,[170][171] hoặc từ sự suy sụp hấp dẫn của sao có khối lượng rất lớn trong vụ nổ siêu tân tinh.[172]
Đa số các chớp có thời gian ghi nhận được lớn hơn khoảng 2 giây và phân loại vào nhóm chớp tia gamma kéo dài, và khoảng 30% các quan sát là những chớp diễn ra ngắn hơn 2 giây hay chớp tia gamma ngắn.[169] Chớp tia gamma kéo dài có nguồn gốc từ quá trình suy sụp hấp dẫn của sao khối lượng rất lớn, như các sao khổng lồ xanh trong các vùng sản sinh sao.[172] Đặc biệt, một trong những chớp gamma có năng lượng lớn nhất, GRB 110328A, kéo dài tới hàng tháng nằm ở một thiên hà cách xa 3,8 tỷ năm ánh sáng có thể là do một lỗ đen siêu khối lượng xé tan và hấp thụ dần một sao lùn trắng quay gần nó.[173]
Dựa vào tính chất của chớp gamma như thời gian xảy ra, năng lượng phát ra và biểu đồ cường độ thu được mà có thể suy đoán ra nguồn gốc những chớp này từ những chùm tia tương đối tính phát ra từ lỗ đen, hay từ quá trình hình thành lên lỗ đen hoặc sự sáp nhập từ hai sao neutron.[169][171][172]
Hiệu ứng của trường hấp dẫn mạnh

Một tính chất khác của lỗ đen so với các thiên thể đặc cho phép phát hiện sự tồn tại của nó, đó là hiệu ứng của trường hấp dẫn tác động mạnh hơn lên không thời gian bao quanh nó. Một trong những hiệu ứng này là thấu kính hấp dẫn: Một vật thể lớn uốn cong không thời gian bao quanh nó khiến cho các tia sáng bị lệch đường đi giống như tác động của các thấu kính quang học. Hiện tại đã có một số dự án khảo sát phát hiện hiệu ứng thấu kính hấp dẫn yếu, trong đó tia sáng chỉ bị lệch vài giây cung. Tuy vậy, cho đến nay chưa thể chụp ảnh được trực tiếp hiệu ứng này đối với lỗ đen.[174] Một cách khác để quan sát hiệu ứng thấu kính hấp dẫn là thông qua ánh sáng phát ra từ những ngôi sao quay quanh lỗ đen. Hiện nay các nhà thiên văn đang thực hiện quan sát tính chất này đối với các sao quay trong vùng Sagittarius A*, mặc dù hiệu ứng là rất nhỏ.[174]
Phương pháp quan trắc trực tiếp khác đó là phát hiện sóng hấp dẫn phát ra từ hệ chứa lỗ đen, ví dụ như các thiên thể đặc quay quanh nó và cuối cùng bị hút về phía lỗ đen. Bằng cách làm phù hợp dữ liệu quan trắc so với tiên đoán của thuyết tương đối tổng quát cho phép tính ra chính xác khối lượng và mô men động lượng của vật thể trung tâm, cũng như thực hiện song song việc kiểm nghiệm thuyết tương đối rộng trong trường hấp dẫn mạnh.[175] Sóng hấp dẫn đã được đo trực tiếp phát ra từ hệ hai lỗ đen khối lượng sao do đài quan trắc LIGO thu được vào ngày 14 tháng 9 năm 2015. Nhóm Hợp tác Khoa học LIGO đã không tìm thấy sự sai khác trong phạm vi sai số thống kê giữa những tiên đoán của thuyết tương đối rộng và kết quả đo được từ sự kiện GW150914.[149] ESA đang có kế hoạch xây dựng ăng ten giao thoa kế eLISA trên vũ trụ nhằm phát hiện trực tiếp sóng hấp dẫn ở những tần số thấp hơn so với các thiết bị mặt đất...
Khả năng khác
Kết luận tồn tại lỗ đen khối lượng sao dựa trên tính toán lý thuyết về giới hạn trên của khối lượng sao neutron. Giá trị này lại phụ thuộc vào giả thuyết về tính chất của vật chất trong trạng thái mật độ cao. Do vậy, những pha mới ngoại lai của vật chất cho phép khối lượng giới hạn cao hơn ở các sao đặc.[64] Một trong số đó gồm sao quark với lõi chứa các hạt quark "tự do" ở mật độ rất cao,[176] hay các mô hình siêu đối xứng trong vật lý hạt tiên đoán sự tồn tại của loại sao Q.[177] Một số lý thuyết mở rộng của Mô hình chuẩn với giả sử các hạt preon cấu thành lên hạt quark và lepton, và dẫn đến giả thuyết tồn tại sao preon với khối lượng cao hơn hẳn sao neutron.[178] Những mô hình này có khả năng giải thích thay thế cho lỗ đen khối lượng sao ở một số quan trắc về các thiên thể đặc trong vũ trụ. Tuy nhiên, theo chứng minh từ thuyết tương đối rộng thì loại sao nào cũng có giới hạn khối lượng trên, và vì thế các mô hình đều dẫn tới sự hình thành lỗ đen.[64]
Vì mật độ trung bình khối lượng của lỗ đen bên trong bán kính Schwarzschild tỉ lệ nghịch với bình phương khối lượng của nó, các lỗ đen siêu khổng lồ có mật độ trung bình nhỏ hơn của lỗ đen khối lượng sao (mật độ trung bình của lỗ đen cỡ 108 M![]() gần bằng khối lượng riêng của nước).[64] Hệ quả là, có những mô hình thay thế khác được đưa ra, mặc dù mô hình lỗ đen siêu khối lượng phù hợp gần với các quan sát thiên văn vật lý. Ví dụ, một khối lượng lớn tập trung trong vùng không gian nhỏ được giải thích bằng việc mô hình hóa một đám lớn các vật thể tối tập trung quanh nhau. Tuy nhiên, mô hình này không ổn định về mặt động lực học để thay thế cho khả năng vùng đó chứa một lỗ đen siêu khối lượng.[64]
gần bằng khối lượng riêng của nước).[64] Hệ quả là, có những mô hình thay thế khác được đưa ra, mặc dù mô hình lỗ đen siêu khối lượng phù hợp gần với các quan sát thiên văn vật lý. Ví dụ, một khối lượng lớn tập trung trong vùng không gian nhỏ được giải thích bằng việc mô hình hóa một đám lớn các vật thể tối tập trung quanh nhau. Tuy nhiên, mô hình này không ổn định về mặt động lực học để thay thế cho khả năng vùng đó chứa một lỗ đen siêu khối lượng.[64]
Sự tồn tại của các lỗ đen khối lượng sao và khổng lồ trong vũ trụ hàm ý thuyết tương đối tổng quát không miêu tả tốt trạng thái và bản chất của kì dị hấp dẫn trong lỗ đen, và có lẽ do lý thuyết lỗ đen chưa kết hợp được với tính chất của cơ học lượng tử. Lý thuyết về hấp dẫn lượng tử có thể sẽ loại bỏ được những vùng kì dị hay chân trời sự kiện và do vậy theo định nghĩa sẽ không có lỗ đen nữa.[179] Dựa trên tính toán trong những tình huống cụ thể của lý thuyết dây, cho kết quả lỗ đen đơn lẻ không còn chứa biên chân trời hay kì dị hấp dẫn, nhưng đối với quan sát viên thuộc miêu tả của vật lý phi lượng tử, trên trung bình, họ vẫn trông thấy những tính chất này giống như trong miêu tả của thuyết tương đối rộng.[180]
Những vấn đề lý thuyết
Ngoài một số mục tiêu như miêu tả vùng kì dị hấp dẫn bằng thuyết hấp dẫn lượng tử cũng như chứng minh hay bác bỏ giả thuyết kiểm duyệt vũ trụ của Penrose, có những vấn đề lý thuyết liên quan đến lỗ đen như sau.
Phỏng đoán vòng
Năm 1972, Thorne nêu ra phỏng đoán vòng (hoop conjecture), rằng khi nén một vật xuống kích cỡ nhỏ hơn một chu vi giới hạn theo mọi hướng thì nó sẽ hình thành lên lỗ đen. Chu vi giới hạn này thường là vòng tròn có bán kính Schwarzschild liên hệ với khối lượng của vật.
Phỏng đoán vòng có một số khía cạnh khi xét vật thể trong không gian nhiều chiều và có khả năng liên quan đến phỏng đoán kiểm duyệt vũ trụ về kì dị hấp dẫn trần trụi cũng như quá trình hình thành lỗ đen vi mô.[62]
Entropy và nhiệt động lực học
Năm 1971, Hawking chứng minh dưới những điều kiện chung[Ct 3] tổng diện tích của chân trời sự kiện của bất kỳ một lỗ đen cổ điển nào không thể giảm, ngay cả khi chúng sáp nhập hoặc va chạm.[181] Kết quả này, ngày nay gọi là định luật 2 của cơ học lỗ đen, rất giống với định luật hai của nhiệt động lực học, nói rằng tổng entropy của một hệ không bao giờ giảm. Và như một vật thể trong vật lý cổ điển tại độ không tuyệt đối, tương ứng với lỗ đen có entropy bằng 0. Nếu có một lỗ đen mà entropy bằng 0, định luật hai của nhiệt động lực học sẽ bị vi phạm khi vật chất có entropy từ bên ngoài rơi vào lỗ đen này, khiến cho tổng entropy của toàn bộ vũ trụ giảm đi. Do vậy, Bekenstein đề xuất lỗ đen phải có entropy - cũng như nhiệt độ khác 0, và giá trị này tỷ lệ với diện tích chân trời sự kiện.[182]
Sự liên kết với nhiệt động học được củng cố thêm khi Hawking khám phá ra lý thuyết trường lượng tử trong không thời gian cong tiên đoán lỗ đen phát ra bức xạ tại nhiệt độ nhất định giống như bức xạ của vật đen tuyệt đối. Dường như điều này vi phạm định luật hai của cơ học lỗ đen, bởi vì bức xạ Hawking sẽ mang năng lượng của lỗ đen đi và khiến cho lỗ đen giảm khối lượng, dẫn đến giảm entropy. Tuy nhiên, bức xạ cũng mang entropy ra khỏi lỗ đen, và có thể chứng minh dưới những giả sử tổng quát rằng tổng entropy của vật chất bao quanh lỗ đen cộng với 1/4 diện tích chân trời sự kiện - đo theo đơn vị Planck - luôn luôn tăng (phải cộng cả vật chất bao quanh lỗ đen bởi vì bức xạ Hawking xuất hiện khi cặp hạt vật chất - phản vật chất sinh ra trong chân không, hạt phản vật chất rơi vào lỗ đen còn hạt vật chất thoát ra ngoài dưới dạng bức xạ). Điều này cho phép thiết lập ra định luật thứ nhất của cơ học lỗ đen tương tự như định luật thứ nhất của nhiệt động lực học, với khối lượng có vai trò như năng lượng, hấp dẫn bề mặt như nhiệt độ và diện tích như entropy.[182]
Một trong những đặc điểm khác thường đó là entropy của lỗ đen tỷ lệ với diện tích hơn là thể tích của nó, do thông thường entropy là một đại lượng mở rộng tỷ lệ tuyến tính với thể tích của hệ. Tính chất kỳ lạ này đưa Gerard 't Hooft và Leonard Susskind dẫn đến giả thuyết về nguyên lý toàn ảnh, nói rằng bất cứ điều gì xảy ra bên trong không thời gian bao bởi vùng thể tích có thể được miêu tả bằng dữ liệu trên biên của thể tích đó.[183]
Mặc dù có thể áp dụng thuyết tương đối rộng trong tính toán bán cổ điển về entropy của lỗ đen, nhưng nó lại mang đến định nghĩa không chặt chẽ. Trong cơ học thống kê, entropy được hiểu là đếm số cấu hình vi mô của một hệ có cùng những đại lượng vĩ mô (như khối lượng, điện tích, áp suất, vv.). Một khi chưa có lý thuyết hấp dẫn lượng tử, các nhà vật lý không thể thực hiện những phép đếm này cho lỗ đen. Một số cách khắc phục đã được đưa ra trên con đường họ đi đến hấp dẫn lượng tử. Năm 1995, Andrew Strominger và Cumrun Vafa chứng minh từ cách đếm các trạng thái vi mô của một lỗ đen cụ thể miêu tả bởi mô hình siêu đối xứng trong thuyết dây cho phép tính ra entropy Bekenstein–Hawking.[184] Từ đó, các nhà vật lý lý thuyết đưa ra một vài kết quả tương tự cho những lỗ đen khác nhau trong cả thuyết dây lẫn những thuyết khác về hấp dẫn lượng tử như hấp dẫn lượng tử vòng nhằm khắc phục định nghĩa entropy cho lỗ đen.[185]
Nghịch lý thông tin bị mất
Bởi vì chỉ cần ba tham số đủ để miêu tả lỗ đen phi lượng tử, hầu hết thông tin về vật chất rơi vào lỗ đen đều biến mất dưới chân trời sự kiện. Người ở bên ngoài không thể biết nó hình thành từ những ngôi sao hay từ tàu không gian, bàn ghế, máy tính, ti vi..., bởi người đó chỉ đo được khối lượng, điện tích và mô men động lượng của lỗ đen. Trong một thời gian dài, các nhà vật lý cho rằng lỗ đen làm mất thông tin, mặc dù thông tin có thể tồn tại bên trong lỗ đen nhưng người ngoài không thể biết được trong đó có gì. Tuy nhiên, theo lý thuyết thì lỗ đen dần dần phát ra bức xạ Hawking và sau một thời gian rất lâu nó bốc hơi (đối với các lỗ đen vĩ mô). Sự bốc hơi này dường như không giải thoát ra bất kỳ thông tin gì về những thứ hình thành lên và đã rơi vào lỗ đen, có nghĩa là về nguyên lý thông tin bị mất mãi mãi.[186]
Trong thời gian dài, câu hỏi liệu thông tin có thực sự bị mất trong lỗ đen (nghịch lý thông tin bị mất bởi lỗ đen) đã chia cộng đồng các nhà lý thuyết lỗ đen thành hai nhóm (xem Vụ cá cược Thorne–Hawking–Preskill). Trong cơ học lượng tử, thông tin bị mất tương ứng với sự vi phạm tính chất sống còn của lý thuyết đó là nguyên lý đơn vị (unitarity) - nguyên lý giới hạn về sự tiến triển của một hệ lượng tử đảm bảo tổng các xác suất của mọi biến cố khả dĩ cho một sự kiện luôn luôn phải bằng 1 - hay nghịch lý thông tin vi phạm định luật bảo toàn xác suất. Ngoài ra, nếu nguyên lý đơn vị bị vi phạm còn dẫn đến định luật bảo toàn năng lượng không còn đúng.[187]
Hawking cá rằng thông tin quả thực biến mất khi mọi thứ bị phá hủy tại vùng kì dị hấp dẫn, còn Gerard 't Hooft và Leonard Susskind cho rằng có một cơ chế nào đó lấy lại thông tin ẩn dưới chân trời sự kiện.[188][189] Năm 2004, Hawking đăng một bài báo chứng minh các thăng giáng lượng tử tại chân trời sự kiện cho phép lý giải nghịch lý và ông thừa nhận thông tin không bị mất cũng như nhận thua trong vụ cá cược với một bên là Preskill và bên kia là Thorne cùng Hawking.[190] Trong cuốn sách của ông, Susskind lập luận là nguyên lý toàn ảnh kết hợp với thuyết dây có thể lý giải thành công nghịch lý này.[188]
Cho đến nay, các công trình lý thuyết chứng tỏ quả thực thông tin và nguyên lý đơn vị được bảo toàn trong cách tiếp cận hấp dẫn lượng tử cho nghịch lý này.[191]
Nghịch lý tường lửa
Theo miêu tả của lý thuyết trường lượng tử trong không thời gian cong, từng bức xạ riêng lẻ của bức xạ Hawking có sự tham gia của hai hạt lượng tử trong trạng thái vướng víu lẫn nhau. Hạt thoát ra ngoài chân trời sự kiện lỗ đen được gán cho là lượng tử của bức xạ Hawking; hạt rơi vào lỗ đen bị lỗ đen nuốt mất. Theo dự đoán của Hawking, một lỗ đen hình thành từ một khoảng thời gian hữu hạn trong quá khứ sẽ cuối cùng bốc hơi hoàn toàn trong khoảng thời gian hữu hạn ở tương lai.[192] Do vậy, nó sẽ chỉ phát ra một lượng hữu hạn thông tin mã hóa bởi bức xạ Hawking. Giả sử ở thời gian , có hơn một nửa thông tin đã phát ra ngoài. Theo như nghiên cứu được chấp thuận rộng rãi bởi các nhà vật lý Don Page[193][194] và Leonard Susskind, một hạt phát ra bên ngoài ở thời điểm phải bị vướng víu với mọi hạt lượng tử của bức xạ Hawking mà lỗ đen đã phát ra trước đó. Điều này dẫn tới một nghịch lý là: theo nguyên lý "một cặp vướng víu" ("monogamy of entanglement" principle) đòi hỏi rằng, như ở bất kỳ một hệ lượng tử nào, hạt thoát ra ngoài không thể vướng víu hẳn toàn bộ với hai hệ độc lập ở cùng một thời điểm; mặc dù thể ở đây hạt bay ra ngoài dường như vướng víu với cả hạt rơi vào trong và, một cách độc lập, với cả các bức xạ Hawking trong quá khứ.[192]
Để lý giải được nghịch lý này, có thể các nhà vật lý cuối cùng buộc phải từ bỏ một trong ba lý thuyết đã được kiểm chứng: nguyên lý tương đương của Einstein, nguyên lý unita trong cơ học lượng tử (tổng xác suất của mọi kết quả khả dĩ của mọi sự kiện luôn bằng 1), hoặc lý thuyết trường lượng tử hiện nay. Một cách giải thích, mà vi phạm nguyên lý tương đương, đó là tồn tại một mặt cầu lửa (tường lửa, "firewall") bao quanh chân trời sự kiện mà phá hủy mọi hạt rơi qua biên giới này.[195] Trong một phân tích các dữ liệu năm 2016 đo được bởi LIGO (GW150914, GW151226 và LVT151012) cho thấy một dấu hiệu chưa chắc chắn về độ vọng sau va chạm hai hố đen gây bởi chân trời sự kiện mờ (fuzzy event horizon); những tiếng vọng này có thể do bởi tường lửa hoặc theo lý thuyết quả bóng mờ (fuzzball theories, trong lý thuyết dây) nhưng tiếng vọng này không thể xuất hiện trong thuyết tương đối tổng quát. Trong tương lai, khi có thêm nhiều sự kiện sóng hấp dẫn đo được bởi LIGO và những trạm khác, các dữ liệu sẽ cho biết liệu những độ vọng này chỉ là nhiễu ngẫu nhiên, hay quả thực chúng là chứng cứ cho sự vi phạm của thuyết tương đối rộng cổ điển.[196]
Lỗ đen trong khoa học viễn tưởng
Các đặc điểm và tính chất vật lý của lỗ đen được nhiều tác giả sử dụng đưa vào những truyện khoa học viễn tưởng trước thập niên 1960, trước khi thuật ngữ này ra đời và cả sau khi những hiểu biết khoa học về nó trở nên đầy đủ hơn. Nó cũng xuất hiện trong các bộ phim khoa học giả tưởng, manga và game.[197]
Ví dụ, tác phẩm "The City and the Stars" (1956) của Arthur C. Clarke, có nói về một vật thể nhân tạo không thể bị phá hủy và nó bị giam giữ ở rìa thiên hà. Tác giả gọi vật thể giống như ngôi sao đó là "mặt trời đen".[198] "Kyrie" (1968), truyện ngắn của Poul Anderson, nói về một đoàn thám hiểm đến "vùng lõi sau vụ nổ siêu tân tinh".[199] Cuốn Lược sử thời gian (1988) của Stephen Hawking ngoài thảo luận về những tính chất của lỗ đen ông cũng nhắc đến viễn cảnh du hành thời gian nhờ đến nó hoặc thông qua lỗ sâu.[200]
Bộ phim Star Trek (2009), có cảnh nói về nhân vật Nero sử dụng "vật chất đỏ" nhằm tạo ra một lỗ đen để phá hủy hành tinh Vulcan.[201] Trong một tập phim của seri 'Star Trek: Voyager', đoàn du hành đã lái tàu vũ trụ băng qua chân trời sự kiện và bị mắc kẹt ở bên trong.[202]
Trong bộ manga InuYasha, nhân vật Miroku với bên tay phải có một Phong huyệt với khả năng hút tất cả mọi thứ giống như lỗ đen.
Trong game Mass Effect 2, người chơi được trang bị loại súng "M-490 Blackstorm" hay "black hole gun" với khả năng tạo ra kì dị hấp dẫn giống như lỗ đen nhằm hút mọi thứ vào trong.[203]
Trong Interstellar (2014) của Christopher Nolan, nhân vật Cooper cùng phi hành đoàn phải đi qua một lỗ sâu (worm hole) để đến các hành tinh mới khác nhằm đi tìm hành tinh - ngôi nhà mới cho loài người - các điều kiện sống trên Trái Đất dần trở nên khắc nghiệt không còn thích hợp cho loài người sinh sống. Lỗ đen trong phim bẻ cong không gian, khiến cho nó có dạng hình cầu, và làm giãn nở thời gian của các hành tinh gần nó. Lỗ đen còn có những điểm kì dị cho ta các không gian năm chiều. Cooper cho rằng cái lỗ đen gần sao Thổ ấy và các không gian năm chiều là thành phẩm của loài người trong tương lai.
Xem thêm
Chú thích
- ↑ Tập hợp mọi đường đi khả dĩ, hay chính xác hơn phần nón ánh sáng tương lai chứa mọi tuyến thế giới (world line) khả dĩ (trong hình này các nón ánh sáng biểu diễn bởi lưới màu vàng/xanh nhạt), bị nghiêng đi trong hệ tọa độ Eddington–Finkelstein (biểu đồ này là phiên bản "đơn giản" của biểu đồ hệ tọa độ Eddington–Finkelstein), nhưng trong những hệ tọa độ khác nón ánh sáng không bị nghiêng như ở biểu đồ này, ví dụ trong hệ tọa độ Schwarzschild chúng chỉ bị thu hẹp đi khi càng tiếp cận gần chân trời sự kiện, và trong hệ tọa độ Kruskal–Szekeres nón ánh sáng không thay đổi hình dạng hay hướng ở mọi điểm trong hệ tọa độ này.[74]
- ↑ Điều này chỉ đúng cho không thời gian 4 chiều. Đối với những chiều cao hơn thì có thể tồn tại dạng chân trời hình vòng xuyến.[80][81]
- ↑ Đặc biệt, ông giả sử rằng mọi vật chất thỏa mãn điều kiện năng lượng yếu.
Tham khảo
- ↑
The Event Horizon Telescope Collaboration; et al. (ngày 10 tháng 4 năm 2019), "First M87 Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole", The Astrophysical Journal, 875 (1), doi:10.3847/2041-8213/ab0ec7 Dùng et al. trong:
|author=(trợ giúp) - ↑ First-ever picture of a black hole, Hiệp hội Max Planck, 10 tháng 4 năm 2019, truy cập 10 tháng 4 năm 2019
- ↑ "Black Hole Image Makes History", NASA, 10 tháng 4 năm 2019, truy cập 11 tháng 4 năm 2019
|first=missing|last=(trợ giúp) - ↑ a b "Black hole - Definition of black hole in English by Oxford Dictionaries", Oxforddictionaries
- ↑ Wald 1984, tr. 299–300
- ↑ a b "What is a black hole?", Heather R. Smith, NASA, ngày 30 tháng 8 năm 2009, truy cập ngày 22 tháng 5 năm 2013
- ↑ Schutz, Bernard F. (2003), Gravity from the ground up, Cambridge University Press, tr. 110, ISBN 0-521-45506-5
- ↑ Davies, P. C. W. (1978), "Thermodynamics of Black Holes" (PDF), Reports on Progress in Physics, 41 (8): 1313–1355, Bibcode:1978RPPh...41.1313D, doi:10.1088/0034-4885/41/8/004, truy cập ngày 9 tháng 5 năm 2013
- ↑ a b c Schwarzschild, K. (1916), "Über das Gravitationsfeld eines Massenpunktes nach der Einsteinschen Theorie", Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften, 7: 189–196CS1 maint: ref=harv (link) and Schwarzschild, K. (1916), "Über das Gravitationsfeld eines Kugel aus inkompressibler Flüssigkeit nach der Einsteinschen Theorie", Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften, 18: 424–434CS1 maint: ref=harv (link)
- ↑ D. Finkelstein (1958), "Past-Future Asymmetry of the Gravitational Field of a Point Particle", Phys. Rev., 110 (4): 965–967, Bibcode:1958PhRv..110..965F, doi:10.1103/PhysRev.110.965
- ↑ a b "NASA's NuSTAR Helps Solve Riddle of Black Hole Spin", Whitney Clavin & J.D. Harrington, NASA, truy cập ngày 19 tháng 5 năm 2013
- ↑ a b c Gillessen, S.; Eisenhauer, F.; Trippe, S.; et al. (2009), "Monitoring Stellar Orbits around the Massive Black Hole in the Galactic Center", The Astrophysical Journal, 692 (2): 1075, arXiv:0810.4674, Bibcode:2009ApJ...692.1075G, doi:10.1088/0004-637X/692/2/1075
- ↑ "What is quantum gravity?", Leron Borsten, Physics World, ngày 9 tháng 5 năm 2013, truy cập ngày 18 tháng 5 năm 2013
- ↑ a b c d Abbott, B.P.; et al. (2016), "Observation of Gravitational Waves from a Binary Black Hole Merger", Phys. Rev. Lett., 116: 061102, arXiv:1602.03837, Bibcode:2016PhRvL.116f1102A, doi:10.1103/PhysRevLett.116.061102, PMID 26918975
- ↑ Michell, J. (1784), "On the Means of Discovering the Distance, Magnitude, &c. of the Fixed Stars, in Consequence of the Diminution of the Velocity of Their Light, in Case Such a Diminution Should be Found to Take Place in any of Them, and Such Other Data Should be Procured from Observations, as Would be Farther Necessary for That Purpose", Philosophical Transactions of the Royal Society, 74 (0): 35–57, Bibcode:1784RSPT...74...35M, doi:10.1098/rstl.1784.0008, JSTOR 106576CS1 maint: ref=harv (link)
- ↑ Gillispie, C. C. (2000), Pierre-Simon Laplace, 1749–1827: a life in exact science, Princeton paperbacks, Princeton University Press, tr. 175, ISBN 0-691-05027-9
- ↑ Israel, W. (1989), "Dark stars: the evolution of an idea", trong Hawking, S. W.; Israel, W. (bt.), 300 Years of Gravitation, Cambridge University Press, ISBN 978-0-521-37976-2
- ↑ Thorne 1994, tr. 123–124
- ↑ Droste, J. (1917), "On the field of a single centre in Einstein's theory of gravitation, and the motion of a particle in that field" (PDF), Proceedings Royal Academy Amsterdam (Royal Netherlands Academy of Arts and Sciences - KNAW), 19 (1): 197–215CS1 maint: ref=harv (link)
- ↑ Jean Eisenstaedt; A.J. Kox (ngày 7 tháng 2 năm 1992), Studies in the History of General Relativity, Springer, tr. 39–42, ISBN 978-0-8176-3479-7, truy cập ngày 19 tháng 5 năm 2013
- ↑ 't Hooft, G. (2009), Introduction to the Theory of Black Holes (PDF), Institute for Theoretical Physics / Spinoza Institute, tr. 47–48
- ↑ Venkataraman, G. (1992), Chandrasekhar and his limit, Universities Press, tr. 86-89, ISBN 81-7371-035-X
- ↑ Detweiler, S. (1981), "Resource letter BH-1: Black holes", American Journal of Physics, 49 (5): 394–400, Bibcode:1981AmJPh..49..394D, doi:10.1119/1.12686CS1 maint: ref=harv (link)
- ↑ Harpaz, A. (1994), Stellar evolution, A K Peters, Ltd., tr. 105, ISBN 1-56881-012-1
- ↑ a b Oppenheimer, J. R.; Volkoff, G. M. (1939), "On Massive Neutron Cores", Physical Review, 55 (4): 374–381, Bibcode:1939PhRv...55..374O, doi:10.1103/PhysRev.55.374CS1 maint: ref=harv (link)
- ↑ R.C. Tolman (1939), "Static Solutions of Einstein's Field Equations for Spheres of Fluid", Physical Review, 55 (4): 364–373, Bibcode:1939PhRv...55..364T, doi:10.1103/PhysRev.55.364
- ↑ Ruffini, R.; Wheeler, J. A. (1971), "Introducing the black hole" (PDF), Physics Today (1): 30–41CS1 maint: ref=harv (link)
- ↑ a b "What would it look like to fall into a black hole?", Stephen Battersby, Newscientist, 1 tháng 4 năm 2009, truy cập 18 tháng 4 năm 2013
- ↑ a b "Journey to a black hole - Drop a clock into a black hole", Staff, Hubblesite.org, truy cập ngày 19 tháng 5 năm 2013
- ↑ Finkelstein, D. (1958), "Past-Future Asymmetry of the Gravitational Field of a Point Particle", Physical Review, 110 (4): 965–967, Bibcode:1958PhRv..110..965F, doi:10.1103/PhysRev.110.965CS1 maint: ref=harv (link)
- ↑ Kruskal, M. (1960), "Maximal Extension of Schwarzschild Metric", Physical Review, 119 (5): 1743, Bibcode:1960PhRv..119.1743K, doi:10.1103/PhysRev.119.1743
- ↑ Thorne, Kip (2003), "Warping spacetime", The future of theoretical physics and cosmology: celebrating Stephen Hawking's 60th birthday, Cambridge University Press, tr. 74, ISBN 0-521-82081-2, Trang 74
- ↑ Hewish, A.; et al. (1968), "Observation of a Rapidly Pulsating Radio Source", Nature, 217 (5130): 709–713, Bibcode:1968Natur.217..709H, doi:10.1038/217709a0CS1 maint: ref=harv (link)
- ↑ Pilkington, J. D. H.; et al. (1968), "Observations of some further Pulsed Radio Sources", Nature, 218 (5137): 126–129, Bibcode:1968Natur.218..126P, doi:10.1038/218126a0CS1 maint: ref=harv (link)
- ↑ Hewish, A. (1970), "Pulsars", Annual Review of Astronomy and Astrophysics, 8 (1): 265–296, Bibcode:1970ARA&A...8..265H, doi:10.1146/annurev.aa.08.090170.001405
- ↑ Newman, E. T.; et al. (1965), "Metric of a Rotating, Charged Mass", Journal of Mathematical Physics, 6 (6): 918, Bibcode:1965JMP.....6..918N, doi:10.1063/1.1704351
- ↑ Israel, W. (1967), "Event Horizons in Static Vacuum Space-Times", Physical Review, 164 (5): 1776, Bibcode:1967PhRv..164.1776I, doi:10.1103/PhysRev.164.1776
- ↑ Carter, B. (1971), "Axisymmetric Black Hole Has Only Two Degrees of Freedom", Physical Review Letters, 26 (6): 331, Bibcode:1971PhRvL..26..331C, doi:10.1103/PhysRevLett.26.331
- ↑ Carter, B. (1977), "The vacuum black hole uniqueness theorem and its conceivable generalisations", Proceedings of the 1st Marcel Grossmann meeting on general relativity, tr. 243–254
- ↑ Robinson, D. (1975), "Uniqueness of the Kerr Black Hole", Physical Review Letters, 34 (14): 905, Bibcode:1975PhRvL..34..905R, doi:10.1103/PhysRevLett.34.905
- ↑ a b Heusler, M. (1998), "Stationary Black Holes: Uniqueness and Beyond", Living Reviews in Relativity, 1 (6), truy cập ngày 10 tháng 8 năm 2012CS1 maint: ref=harv (link) A bot will complete this citation soon. Click here to jump the queue. arΧiv:1205.6112.
- ↑ Belinskii, V.; Khalatnikov, I.; Lifschitz, E. (1970), "Oscillatory approach to a singular point in the relativistic cosmology", Adv. In Phys., 19 (80): 525–573, Bibcode:1970AdPhy..19..525B, doi:10.1080/00018737000101171
- ↑ a b Penrose, R. (1965), "Gravitational Collapse and Space-Time Singularities", Physical Review Letters, 14 (3): 57, Bibcode:1965PhRvL..14...57P, doi:10.1103/PhysRevLett.14.57CS1 maint: ref=harv (link)
- ↑ Ford, L. H. (2003), "The Classical Singularity Theorems and Their Quantum Loopholes", International Journal of Theoretical Physics, 42 (6): 1219, doi:10.1023/A:1025754515197
- ↑ Bardeen, J. M.; Carter, B.; Hawking, S. W. (1973), "The four laws of black hole mechanics", Communications in Mathematical Physics, 31 (2): 161–170, Bibcode:1973CMaPh..31..161B, doi:10.1007/BF01645742, MR 0334798, Zbl 1125.83309CS1 maint: ref=harv (link)
- ↑ a b c Hawking, S. W. (1974), "Black hole explosions?", Nature, 248 (5443): 30–31, Bibcode:1974Natur.248...30H, doi:10.1038/248030a0CS1 maint: ref=harv (link)
- ↑ Quinion, M. (ngày 26 tháng 4 năm 2008), "Black Hole", World Wide Words, truy cập ngày 17 tháng 6 năm 2008
- ↑ Piotr Chrusciel (2010), How many different kinds of black holes are there?, Max Planck Institute for Gravitational Physics, truy cập ngày 19 tháng 5 năm 2013
- ↑ Carroll 2004, tr. 253
- ↑ "Space time and spin", James Overduin, Stanford University, ngày 10 tháng 1 năm 2008, truy cập ngày 18 tháng 4 năm 2013
- ↑ Thorne, K. S.; Price, R. H. (1986), Black holes: the membrane paradigm, Yale University Press, tr. Editor's preface, ISBN 978-0-300-03770-8
- ↑ Anderson, Warren G. (1996), "The Black Hole Information Loss Problem", Usenet Physics FAQ, truy cập ngày 24 tháng 3 năm 2009
- ↑ Preskill, J. (ngày 21 tháng 10 năm 1994), Black holes and information: A crisis in quantum physics (PDF)
- ↑ Hawking & Ellis 1973, Appendix B
- ↑ "Dictionary - Birkhoff's theorem", Markus Pössel, Albert Einstein Institut, truy cập ngày 21 tháng 5 năm 2013
- ↑ Seeds, Michael A.; Backman, Dana E. (2007), Perspectives on Astronomy, Cengage Learning, tr. 167, ISBN 0-495-11352-2
- ↑ Shapiro, S. L.; Teukolsky, S. A. (1983), Black holes, white dwarfs, and neutron stars: the physics of compact objects, John Wiley and Sons, tr. 357, ISBN 0-471-87316-0
- ↑ Naked singularity, Encyclopedia of Math, truy cập ngày 20 tháng 5 năm 2013
- ↑ "Singularity", Markus Pössel, Max Planck Instituts für Gravitationsphysik (Albert Einstein Institut), truy cập ngày 21 tháng 5 năm 2013
- ↑ Wald, R. M. (1997). Bản mẫu:Citation/make link. arΧiv:gr-qc/9710068 [gr-qc].
- ↑ Hazewinkel, Michiel, bt. (2001), "Penrose cosmic censorship", Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
- ↑ a b c Berger, B. K. (2002), "Numerical Approaches to Spacetime Singularities", Living Reviews in Relativity, 5, doi:10.12942/lrr-2002-1, truy cập ngày 4 tháng 8 năm 2007CS1 maint: ref=harv (link)
- ↑ McClintock, J. E.; Shafee, R.; Narayan, R.; Remillard, R. A.; Davis, S. W.; Li, L.-X. (2006), "The Spin of the Near-Extreme Kerr Black Hole GRS 1915+105", Astrophysical Journal, 652 (1): 518–539, arXiv:astro-ph/0606076, Bibcode:2006ApJ...652..518M, doi:10.1086/508457CS1 maint: ref=harv (link)
- ↑ a b c d e f g h i j Celotti, A.; Miller, J. C.; Sciama, D. W. (1999), "Astrophysical evidence for the existence of black holes", Classical and Quantum Gravity, IOP publishing, 16 (12A): A3–A21, arXiv:astro-ph/9912186, doi:10.1088/0264-9381/16/12A/301CS1 maint: ref=harv (link)
- ↑ "Hubble Discovers Black Holes in Unexpected Places", Rebecca Johnson et al, hubblesite.org, 2002, truy cập ngày 18 tháng 4 năm 2013
- ↑ Wald 1984, tr. 124–125
- ↑ Gelino, Dawn M.; Harrison, Thomas E. (2003), "GRO J0422+32: The Lowest Mass Black Hole?", The Astrophysical Journal, IOP publishing, 599 (2): 1254–1259, doi:10.1086/379311CS1 maint: multiple names: authors list (link)
- ↑ "NASA Scientists Identify Smallest Known Black Hole", Robert Naeye, NASA, ngày 1 tháng 4 năm 2008, truy cập ngày 19 tháng 5 năm 2013
- ↑ Shaposhnikov, Nickolai; Titarchuk, Lev (2009), "Determination of black hole masses in galatic black hole binaries using scaling of spectral and variability characteristics", The Astrophysical Journal, 699 (1): 453–468, doi:10.1088/0004-637X/699/1/453, ISSN 0004-637X
- ↑ van den Bosch, Remco C. E.; Gebhardt, Karl; Gültekin, Kayhan; van de Ven, Glenn; van der Wel, Arjen; Walsh, Jonelle L. (2012), "An over-massive black hole in the compact lenticular galaxy NGC 1277", Nature, 491 (7426): 729–731, doi:10.1038/nature11592, ISSN 0028-0836
- ↑ a b M. J. Valtonen; et al. (2008), "A massive binary black-hole system in OJ 287 and a test of general relativity" (PDF), Nature, 452: 851–853, doi:10.1038/nature06896 Dùng et al. trong:
|author=(trợ giúp) - ↑ Nicholas J. McConnell; et al. (2011), "Two ten-billion-solar-mass black holes at the centres of giant elliptical galaxies", Nature, 480 (7376): 215–218, arXiv:1112.1078v1, doi:10.1038/nature10636 Dùng et al. trong:
|author=(trợ giúp) - ↑ Hawking & Ellis 1973, tr. 152
- ↑ Thorne, Misner & Wheeler 1973, tr. 848
- ↑ Wheeler 2007, tr. 179
- ↑ Carroll 2004, Ch. 5.4 và 7.3
- ↑ Carroll 2004, tr. 217
- ↑ Carroll 2004, tr. 218
- ↑ "Inside a black hole", Knowing the universe and its secrets, truy cập ngày 26 tháng 3 năm 2009
- ↑ Emparan, R.; Reall, H. S. (2008), "Black Holes in Higher Dimensions", Living Reviews in Relativity, 11 (6), arXiv:0801.3471, Bibcode:2008LRR....11....6E, truy cập ngày 10 tháng 2 năm 2011
- ↑ Obers, N. A. (2009), Papantonopoulos, Eleftherios (bt.), "Black Holes in Higher-Dimensional Gravity", Lecture Notes in Physics, 769: 211–258, arXiv:0802.0519, doi:10.1007/978-3-540-88460-6
- ↑ hawking & ellis 1973, Ch. 9.3
- ↑ M. P. Hobson; G. P. Efstathiou; A. N. Lasenby (ngày 2 tháng 2 năm 2006), General Relativity: An Introduction for Physicists, Cambridge University Press, tr. 325–, ISBN 978-0-521-82951-9, truy cập ngày 21 tháng 5 năm 2013
- ↑ Carroll 2004, tr. 205
- ↑ Carroll 2004, tr. 264–265
- ↑ Carroll 2004, tr. 252
- ↑ Markus Pössel (2010), Changing places - space and time inside a black hole, Max Planck Institute for Gravitational Physics, truy cập ngày 19 tháng 5 năm 2013
- ↑ Schutz 2009, tr. 299
- ↑ Schutz 2009, tr. 300
- ↑ Lewis, G. F.; Kwan, J. (2007), "No Way Back: Maximizing Survival Time Below the Schwarzschild Event Horizon", Publications of the Astronomical Society of Australia, 24 (2): 46–52, arXiv:0705.1029, Bibcode:2007PASA...24...46L, doi:10.1071/AS07012
- ↑ Wheeler 2007, tr. 182
- ↑ Wald 1984, tr. 212
- ↑ Hamade, R. (1996), "Black Holes and Quantum Gravity", Cambridge Relativity and Cosmology, University of Cambridge, truy cập ngày 26 tháng 3 năm 2009
- ↑ Palmer, D., Ask an Astrophysicist: Black Holes, NASA, truy cập ngày 26 tháng 3 năm 2009
- ↑ a b Avery E. Broderick and Abraham Loeb (2009), "Potrait of a black hole" (PDF), Scientific American, Nature America, Inc, December
- ↑ a b c Edward Teo (2003), "Spherical Photon Orbits Around a Kerr Black Hole" (PDF), General Relativity and Gravitation, Kluwer Academic Publishers, 35 (11): 1909–1926, doi:10.1023/A:1026286607562
- ↑ Schutz 2009, tr. 313-316
- ↑ Nitta, Daisuke; Chiba, Takeshi; Sugiyama, Naoshi (2011), "Shadows of colliding black holes", Physical Review D, 84 (6), arXiv:1106.2425v2, Bibcode:2011PhRvD..84f3008N, doi:10.1103/PhysRevD.84.063008 Bỏ qua tham số chưa biết
|month=(trợ giúp) - ↑ Nemiroff, R. J. (1993), "Visual distortions near a neutron star and black hole", American Journal of Physics, 61 (7): 619, arXiv:astro-ph/9312003, Bibcode:1993AmJPh..61..619N, doi:10.1119/1.17224CS1 maint: ref=harv (link)
- ↑ Nemiroff, R. J.; Becker, P. A.; Wood, K. S. (1993), "Properties of ultracompact neutron stars", Astrophysical Journal, 406 (2): 590-595, Bibcode:1993ApJ...406..590N, doi:10.1086/172471CS1 maint: ref=harv (link)
- ↑ Schutz 2009, tr. 316
- ↑ "Crossection of a rotating black hole", Jillian, gothosenterprises.com, truy cập ngày 20 tháng 5 năm 2013
- ↑ Schutz 2009, tr. 312
- ↑ Carroll 2004, Ch. 6.6
- ↑ Carroll 2004, Ch. 6.7
- ↑ Schutz 2009, tr. 315-316
- ↑ a b c d "Is time travel possible?", Michio Kaku, PBS, truy cập ngày 24 tháng 5 năm 2013
- ↑ a b c d "What happen to you if you fall into a black hole?", Matt McIrvin, truy cập ngày 24 tháng 5 năm 2013
- ↑ Carroll 2004, tr. 222
- ↑ Carroll 2004, tr. 257–259 and 265–266
- ↑ Droz, S.; Israel, W.; Morsink, S. M. (1996), "Black holes: the inside story", Physics World, 9 (1): 34–37, Bibcode:1996PhyW....9...34DCS1 maint: ref=harv (link)
- ↑ Carroll 2004, tr. 266
- ↑ Poisson, E.; Israel, W. (1990), "Internal structure of black holes", Physical Review D, 41 (6): 1796, Bibcode:1990PhRvD..41.1796P, doi:10.1103/PhysRevD.41.1796
- ↑ "How to build a time machine", Stephen Hawking, dailymail.co.uk, truy cập ngày 24 tháng 5 năm 2013
- ↑ Einstein, A. (1939), "On A Stationary System With Spherical Symmetry Consisting of Many Gravitating Masses", Annals of Mathematics, 40 (4): 922–936, doi:10.2307/1968902CS1 maint: ref=harv (link)
- ↑ Thorne 1994, tr. 135
- ↑ a b Jeremy Bernstein (2007), "The Reluctant Father of Black Holes", Scientific American, Nature publishing group, 17: 4–11, doi:10.1038/scientificamerican0407-4sp
- ↑ Kerr, R. P. (2009), "The Kerr and Kerr-Schild metrics", trong Wiltshire, D. L.; Visser, M.; Scott, S. M. (bt.), The Kerr Spacetime, Cambridge University Press, arXiv:0706.1109, ISBN 978-0-521-88512-6
- ↑ Thorne 1994, tr. 138
- ↑ Hawking, S. W.; Penrose, R. (1970), "The Singularities of Gravitational Collapse and Cosmology", Proceedings of the Royal Society A, 314 (1519): 529–548, Bibcode:1970RSPSA.314..529H, doi:10.1098/rspa.1970.0021, JSTOR 2416467 Bỏ qua tham số chưa biết
|month=(trợ giúp)CS1 maint: ref=harv (link) - ↑ a b c Carroll 2004, Section 5.8
- ↑ a b c Rees, M. J.; Volonteri, M. (2007), "Massive black holes: formation and evolution", trong Karas, V.; Matt, G. (bt.), Black Holes from Stars to Galaxies—Across the Range of Masses, Cambridge University Press, tr. 51–58, arXiv:astro-ph/0701512, ISBN 978-0-521-86347-6
- ↑ Penrose, R. (2002), "Gravitational Collapse: The Role of General Relativity" (PDF), General Relativity and Gravitation, 34 (7): 1141, Bibcode:2002GReGr..34.1141P, doi:10.1023/A:1016578408204
- ↑ Carr, B. J. (2005), "Primordial Black Holes: Do They Exist and Are They Useful?", trong Suzuki, H.; Yokoyama, J.; Suto, Y.; Sato, K. (bt.), Inflating Horizon of Particle Astrophysics and Cosmology, Universal Academy Press, arXiv:astro-ph/0511743, ISBN 4-946443-94-0
- ↑ "Colliding Particles Can Make Black Holes", Adrian Cho, Science, ngày 22 tháng 1 năm 2010, truy cập ngày 22 tháng 5 năm 2013
- ↑ a b c Cavaglià, Marco (2010), Particle accelerators as black hole factories?, Viện Vật lý hấp dẫn Max Planck - Viện Albert Einstein, truy cập ngày 22 tháng 5 năm 2013
- ↑ Harada, T. (2006), "Is there a black hole minimum mass?", Physical Review D, 74 (8): 084004, arXiv:gr-qc/0609055, Bibcode:2006PhRvD..74h4004H, doi:10.1103/PhysRevD.74.084004
- ↑ Arkani–Hamed, N.; Dimopoulos, S.; Dvali, G. (1998), "The hierarchy problem and new dimensions at a millimeter", Physics Letters B, 429 (3–4): 263, arXiv:hep-ph/9803315, Bibcode:1998PhLB..429..263A, doi:10.1016/S0370-2693(98)00466-3CS1 maint: ref=harv (link)
- ↑ a b William E. East and Frans Pretorius (2013), "Micro black holes could form at lower-than-expected energies", Phys. Rev. Lett., American Physical Society, 110 (10), arXiv:1210.0443v2, doi:10.1103/PhysRevLett.110.101101CS1 maint: uses authors parameter (link)
- ↑ LHC Safety Assessment Group, Review of the Safety of LHC Collisions (PDF), CERN
- ↑ Vesperini, E.; McMillan, S. L. W.; D'Ercole, A.; et al. (2010), "Intermediate-Mass Black Holes in Early Globular Clusters", The Astrophysical Journal Letters, 713 (1): L41–L44, arXiv:1003.3470, Bibcode:2010ApJ...713L..41V, doi:10.1088/2041-8205/713/1/L41
- ↑ Zwart, S. F. P.; Baumgardt, H.; Hut, P.; et al. (2004), "Formation of massive black holes through runaway collisions in dense young star clusters", Nature, 428 (6984): 724, arXiv:astro-ph/0402622, Bibcode:2004Natur.428..724P, doi:10.1038/nature02448, PMID 15085124
- ↑ O'Leary, R. M.; Rasio, F. A.; Fregeau, J. M.; et al. (2006), "Binary Mergers and Growth of Black Holes in Dense Star Clusters", The Astrophysical Journal, 637 (2): 937, arXiv:astro-ph/0508224, Bibcode:2006ApJ...637..937O, doi:10.1086/498446
- ↑ a b "Luminous disks: How black holes light up their surroundings", Andreas Müller, Albert Einstein Institute, 2010, truy cập ngày 24 tháng 5 năm 2013
- ↑ J. M. Corral-Santana; et al. (2013), "A Black Hole Nova Obscured by an Inner Disk Torus", Science, AAAS, 339 (6123): 1048–1051, doi:10.1126/science.1228222 Dùng et al. trong:
|author=(trợ giúp) - ↑ Koppitz, Michael; et al. (2007), "Recoil Velocities from Equal-Mass Binary-Black-Hole Mergers", Physical Review Letters, 99 (4), arXiv:gr-qc/0701163v2, doi:10.1103/PhysRevLett.99.041102, ISSN 0031-9007 Dùng et al. trong:
|last2=(trợ giúp) - ↑ Page, D. N. (2005), "Hawking radiation and black hole thermodynamics", New Journal of Physics, 7: 203, arXiv:hep-th/0409024, Bibcode:2005NJPh....7..203P, doi:10.1088/1367-2630/7/1/203CS1 maint: ref=harv (link)
- ↑ Carroll 2004, Ch. 9.6
- ↑ "Evaporating black holes?", Einstein online, Max Planck Institute for Gravitational Physics, 2010, truy cập ngày 12 tháng 12 năm 2010
- ↑ Giddings, S. B.; Mangano, M. L. (2008), "Astrophysical implications of hypothetical stable TeV-scale black holes", Physical Review D, 78 (3): 035009, arXiv:0806.3381, Bibcode:2008PhRvD..78c5009G, doi:10.1103/PhysRevD.78.035009
- ↑ Peskin, M. E. (2008), "The end of the world at the Large Hadron Collider?", Physics, 1: 14, Bibcode:2008PhyOJ...1...14P, doi:10.1103/Physics.1.14
- ↑ Misner, Thorne & Wheeler 1973, Ch 33
- ↑ Fichtel, C. E.; Bertsch, D. L.; Dingus, B. L.; et al. (1994), "Search of the energetic gamma-ray experiment telescope (EGRET) data for high-energy gamma-ray microsecond bursts", Astrophysical Journal, 434 (2): 557–559, Bibcode:1994ApJ...434..557F, doi:10.1086/174758CS1 maint: ref=harv (link)
- ↑ Naeye, R., Testing Fundamental Physics, NASA, truy cập ngày 16 tháng 9 năm 2008
- ↑ Event Horizon Telescope, NSF, truy cập ngày 6 tháng 4 năm 2012
- ↑ Overbye, Dennis (ngày 11 tháng 2 năm 2016), "Physicists Detect Gravitational Waves, Proving Einstein Right", New York Times, truy cập ngày 11 tháng 2 năm 2017
- ↑ Abbott, Benjamin P. (ngày 14 tháng 6 năm 2016), "Properties of the binary black hole merger GW150914", Phys. Rev. Lett., LIGO Scientific Collaboration and Virgo Collaboration, 116 (24), arXiv:1602.03840, doi:10.1103/PhysRevLett.116.241102
- ↑ a b Cardoso, V.; Franzin, E.; Pani, P. (2016), "Is the gravitational-wave ringdown a probe of the event horizon?", Physical Review Letters, 116, arXiv:1602.07309, Bibcode:2016PhRvL.116q1101C, doi:10.1103/PhysRevLett.116.171101
- ↑ a b Abbott, Benjamin P.; et al. (ngày 11 tháng 2 năm 2016), "Tests of general relativity with GW150914", Phys. Rev. Lett., LIGO Scientific Collaboration and Virgo Collaboration, 116 (22), doi:10.1103/PhysRevLett.116.221101, truy cập ngày 11 tháng 2 năm 2017 Dùng et al. trong:
|last2=(trợ giúp) - ↑ "Astrophysical Implications of the Binary Black Hole Merger GW150914", Astrophys. J. Lett., LIGO Scientific Collaboration and Virgo Collaboration, 818 (2): L22, arXiv:1602.03846, Bibcode:2016ApJ...818L..22A, doi:10.3847/2041-8205/818/2/L22
- ↑ a b c McClintock, J. E.; Remillard, R. A. (2006), "Black Hole Binaries", trong Lewin, W.; van der Klis, M. (bt.), Compact Stellar X-ray Sources, Cambridge University Press, arXiv:astro-ph/0306213, ISBN 0-521-82659-4 phần 4.1.5.
- ↑ Schutz 2009, tr. 317
- ↑ Winter, L. M.; Mushotzky, R. F.; Reynolds, C. S. (2006), "XMM‐Newton Archival Study of the Ultraluminous X‐Ray Population in Nearby Galaxies", The Astrophysical Journal, 649 (2): 730, arXiv:astro-ph/0512480, Bibcode:2006ApJ...649..730W, doi:10.1086/506579CS1 maint: ref=harv (link)
- ↑ a b c d "Active black hole: Ultra hot cosmic beacons", Andreas Müller, Max Planck Institute for Gravitational Physics, 2006, truy cập ngày 23 tháng 5 năm 2013
- ↑ Bolton, C. T. (1972), "Identification of Cygnus X-1 with HDE 226868", Nature, 235 (5336): 271–273, Bibcode:1972Natur.235..271B, doi:10.1038/235271b0CS1 maint: ref=harv (link)
- ↑ Webster, B. L.; Murdin, P. (1972), "Cygnus X-1—a Spectroscopic Binary with a Heavy Companion ?", Nature, 235 (5332): 37–38, Bibcode:1972Natur.235...37W, doi:10.1038/235037a0CS1 maint: ref=harv (link)
- ↑ Rolston, B. (ngày 10 tháng 11 năm 1997), "The First Black Hole", The bulletin, University of Toronto, lưu trữ từ nguyên tác ngày 2 tháng 5 năm 2008, truy cập ngày 11 tháng 3 năm 2008 Bỏ qua tham số chưa biết
|dead-url=(gợi ý|url-status=) (trợ giúp) - ↑ Shipman, H. L. (ngày 1 tháng 1 năm 1975), "The implausible history of triple star models for Cygnus X-1 Evidence for a black hole", Astrophysical Letters, 16 (1): 9–12, Bibcode:1975ApL....16....9S, doi:10.1016/S0304-8853(99)00384-4CS1 maint: ref=harv (link)
- ↑ Narayan, R.; McClintock, J. (2008), "Advection-dominated accretion and the black hole event horizon", New Astronomy Reviews, 51 (10–12): 733, arXiv:0803.0322, Bibcode:2008NewAR..51..733N, doi:10.1016/j.newar.2008.03.002
- ↑ Schutz 2009, tr. 286
- ↑ NASA scientists identify smallest known black hole, Goddard Space Flight Center, ngày 1 tháng 4 năm 2008, truy cập ngày 14 tháng 3 năm 2009
- ↑ Krolik, J. H. (1999), Active Galactic Nuclei, Princeton University Press, Ch. 1.2, ISBN 0-691-01151-6
- ↑ Sparke, L. S.; Gallagher, J. S. (2000), Galaxies in the Universe: An Introduction, Cambridge University Press, Ch. 9.1, ISBN 0-521-59740-4
- ↑ Kormendy, J.; Richstone, D. (1995), "Inward Bound—The Search For Supermassive Black Holes In Galactic Nuclei", Annual Reviews of Astronomy and Astrophysics, 33 (1): 581–624, Bibcode:1995ARA&A..33..581K, doi:10.1146/annurev.aa.33.090195.003053CS1 maint: ref=harv (link)
- ↑ King, A. (2003), "Black Holes, Galaxy Formation, and the MBH-σ Relation", The Astrophysical Journal Letters, 596 (1): 27–29, arXiv:astro-ph/0308342, Bibcode:2003ApJ...596L..27K, doi:10.1086/379143CS1 maint: ref=harv (link)
- ↑ Ferrarese, L.; Merritt, D. (2000), "A Fundamental Relation Between Supermassive Black Holes and their Host Galaxies", The Astrophysical Journal Letters, 539 (1): 9–12, arXiv:astro-ph/0006053, Bibcode:2000ApJ...539L...9F, doi:10.1086/312838CS1 maint: ref=harv (link)
- ↑ "A Black Hole's Dinner is Fast Approaching", ESO Press Release, truy cập ngày 6 tháng 2 năm 2012
- ↑ a b Ghez, A. M.; Klein, B. L.; Morris, M.; et al. (1998), "High Proper‐Motion Stars in the Vicinity of Sagittarius A*: Evidence for a Supermassive Black Hole at the Center of Our Galaxy", The Astrophysical Journal, 509 (2): 678, arXiv:astro-ph/9807210, Bibcode:1998ApJ...509..678G, doi:10.1086/306528
- ↑ a b c "In a Flash NASA Helps Solve 35-year-old Cosmic Mystery", Staff, NASA, truy cập ngày 23 tháng 5 năm 2013
- ↑ "Ghostly jets seen streaming from Milky Way's core", Ron Cowen, Nature, truy cập ngày 23 tháng 5 năm 2013
- ↑ a b "Study Reveals a Remarkable Symmetry in Black Hole Jets", Francis Reddy, NASA, truy cập ngày 23 tháng 5 năm 2013
- ↑ a b c "Dying Supergiant Stars Implicated in Hours-long Gamma-Ray Bursts", Francis Reddy, NASA, truy cập ngày 23 tháng 5 năm 2013
- ↑ Levan, A. J.; et al. (2011), "An Extremely Luminous Panchromatic Outburst from the Nucleus of a Distant Galaxy", Science, 333 (6039): 199–202, arXiv:1104.3356v1, doi:10.1126/science.1207143, ISSN 0036-8075 Dùng et al. trong:
|last2=(trợ giúp) - ↑ a b Bozza, V. (2010), "Gravitational Lensing by Black Holes", General Relativity and Gravitation (42): 2269–2300, arXiv:0911.2187, Bibcode:2010GReGr..42.2269B, doi:10.1007/s10714-010-0988-2
- ↑ Barack, L.; Cutler, C. (2004), "LISA capture sources: Approximate waveforms, signal-to-noise ratios, and parameter estimation accuracy", Physical Review D (69): 082005, arXiv:gr-qc/0310125, Bibcode:2004PhRvD..69h2005B, doi:10.1103/PhysRevD.69.082005
- ↑ Kovacs, Z.; Cheng, K. S.; Harko, T. (2009), "Can stellar mass black holes be quark stars?", Monthly Notices of the Royal Astronomical Society, 400 (3): 1632–1642, arXiv:0908.2672, Bibcode:2009MNRAS.400.1632K, doi:10.1111/j.1365-2966.2009.15571.x
- ↑ Kusenko, A. (2006). Bản mẫu:Citation/make link. arΧiv:hep-ph/0612159 [hep-ph].
- ↑ Hansson, J.; Sandin, F. (2005), "Preon stars: a new class of cosmic compact objects", Physics Letters B, 616 (1–2): 1, arXiv:astro-ph/0410417, Bibcode:2005PhLB..616....1H, doi:10.1016/j.physletb.2005.04.034
- ↑ Kiefer, C. (2006), "Quantum gravity: general introduction and recent developments", Annalen der Physik, 15 (1–2): 129, arXiv:gr-qc/0508120, Bibcode:2006AnP...518..129K, doi:10.1002/andp.200510175
- ↑ Skenderis, K.; Taylor, M. (2008), "The fuzzball proposal for black holes", Physics Reports, 467 (4–5): Section 2, arXiv:0804.0552, Bibcode:2008PhR...467..117S, doi:10.1016/j.physrep.2008.08.001
- ↑ Hawking, S. W. (1971), "Gravitational Radiation from Colliding Black Holes", Physical Review Letters, 26 (21): 1344–1346, Bibcode:1971PhRvL..26.1344H, doi:10.1103/PhysRevLett.26.1344
- ↑ a b Wald, R. M. (2001), "The Thermodynamics of Black Holes" (PDF), Living Reviews in Relativity, 4 (6), arXiv:gr-qc/9912119, Bibcode:1999gr.qc....12119W, doi:10.12942/lrr-2001-6, truy cập ngày 10 tháng 2 năm 2011
- ↑ 't Hooft, G. (2001), "The Holographic Principle", trong Zichichi, A. (bt.), Basics and highlights in fundamental physics, Subnuclear series, 37, World Scientific, arXiv:hep-th/0003004, ISBN 978-981-02-4536-8
- ↑ Strominger, A.; Vafa, C. (1996), "Microscopic origin of the Bekenstein-Hawking entropy", Physics Letters B, 379 (1–4): 99, arXiv:hep-th/9601029, Bibcode:1996PhLB..379...99S, doi:10.1016/0370-2693(96)00345-0
- ↑ Carlip, S. (2009), "Black Hole Thermodynamics and Statistical Mechanics", Lecture Notes in Physics, 769: 89, arXiv:0807.4520, doi:10.1007/978-3-540-88460-6_3
- ↑ Hawking, S. W., "Does God Play Dice?", www.hawking.org.uk, truy cập ngày 14 tháng 3 năm 2009
- ↑ Giddings, S. B. (1995), The black hole information paradox, arXiv:hep-th/9508151
- ↑ a b Leonard Susskind (ngày 7 tháng 7 năm 2008), "Introduction", The Black Hole War: My Battle with Stephen Hawking to Make the World Safe for Quantum Mechanics, Hachette Inc., ISBN 978-0-316-01640-7, truy cập ngày 5 tháng 8 năm 2012
- ↑ Carroll, Sean (ngày 28 tháng 7 năm 2012), "Lost in Space", Wall Street Journal, truy cập ngày 6 tháng 8 năm 2012
- ↑ Baez, John, This Week's Finds in Mathematical Physics (Week 207), truy cập ngày 25 tháng 9 năm 2012
- ↑ Mathur, S. D. (2011), The information paradox: conflicts and resolutions, arXiv:1201.2079
- ↑ a b Merali, Zeeya (ngày 3 tháng 4 năm 2013), "Astrophysics: Fire in the hole!", Nature, 496: 20–23, doi:10.1038/496020a, truy cập ngày 11 tháng 2 năm 2017
- ↑ Page, Don N. (1993), "Information in black hole radiation", Phys. Rev. Lett., 71: 3743, arXiv:hep-th/9306083, Bibcode:1993PhRvL..71.3743P, doi:10.1103/PhysRevLett.71.3743
- ↑ Page, Don N. (1993), "Average entropy of a subsystem", Phys. Rev. Lett., 71: 1291, arXiv:gr-qc/9305007, Bibcode:1993PhRvL..71.1291P, doi:10.1103/PhysRevLett.71.1291
- ↑ Ouellette, Jennifer (ngày 21 tháng 12 năm 2012), "Black Hole Firewalls Confound Theoretical Physicists", Scientific American, truy cập ngày 29 tháng 10 năm 2013 Originally published in Quanta, ngày 21 tháng 12 năm 2012.
- ↑ Merali, Zeeya (ngày 9 tháng 12 năm 2016), "LIGO black hole echoes hint at general-relativity breakdown", Nature, 540, doi:10.1038/nature.2016.21135
- ↑ Black hole, The Encyclopedia of Science Fiction, ngày 28 tháng 2 năm 2013, truy cập ngày 23 tháng 5 năm 2013
- ↑ Clarke, Arthur C (2001), The City and the Stars, New York: Hachette Book Group USA - Aspect, tr. 264, ISBN 0-446-67796-5
- ↑ Pournelle, Jerry (1978), "Kyrie", Black Holes, Brooklyn NY: Fawcett Publications, tr. 105, 107, ISBN 0-449-23962-4
- ↑ Hawking, Stephen; Lược sử thời gian; Bantam Books, 1988, Chương 6 và 7, ISBN-13 9780553109535; bản tiếng Việt do Cao Chi và Phạm Văn Thiều dịch.
- ↑ Planet Vulcan Gets Owned By Black Hole YouTube
- ↑ Wormholes, Warp Speed and other Weird Things, Oracle Think Quest, truy cập ngày 22 tháng 5 năm 2013
- ↑ M-490 Blackstorm, masseffect.wikia.com, truy cập ngày 23 tháng 5 năm 2013
Đọc thêm
- Sách phổ biến
- Ferguson, Kitty (1991), Black Holes in Space-Time, Watts Franklin, ISBN 0-531-12524-6CS1 maint: ref=harv (link)
- Hawking, Stephen (1988), A Brief History of Time, Bantam Books, Inc, ISBN 0-553-38016-8CS1 maint: ref=harv (link)
- Hawking, Stephen; Penrose, Roger (1996), The Nature of Space and Time, Princeton University Press, ISBN 0-691-03791-4CS1 maint: ref=harv (link)
- Melia, Fulvio (2003), The Black Hole at the Center of Our Galaxy, Princeton U Press, ISBN 978-0-691-09505-9CS1 maint: ref=harv (link)
- Melia, Fulvio (2003), The Edge of Infinity. Supermassive Black Holes in the Universe, Cambridge U Press, ISBN 978-0-521-81405-8CS1 maint: ref=harv (link)
- Pickover, Clifford (1998), Black Holes: A Traveler's Guide, Wiley, John & Sons, Inc, ISBN 0-471-19704-1
- Thorne, Kip S. (1994), Black Holes and Time Warps, Norton, W. W. & Company, Inc, ISBN 0-393-31276-3CS1 maint: ref=harv (link)
- Wheeler, J. Craig (2007), Cosmic Catastrophes (lxb. 2nd), Cambridge University Press, ISBN 0-521-85714-7CS1 maint: ref=harv (link)
- Sách và giáo trình đại học
- Carroll, Sean M. (2004), Spacetime and Geometry, Addison Wesley, ISBN 0-8053-8732-3CS1 maint: ref=harv (link), the lecture notes on which the book was based are available for free from Sean Carroll's website.
- Carter, B. (1973), "Black hole equilibrium states", trong DeWitt, B. S.; DeWitt, C. (bt.), Black HolesCS1 maint: ref=harv (link)
- Chandrasekhar, Subrahmanyan (1999), The Mathematical Theory of Black Holes, Oxford University Press, ISBN 0198503709CS1 maint: ref=harv (link)
- Frolov, V. P.; Novikov, I. D. (1998), Black hole physics, Springer, ISBN 0792351452CS1 maint: ref=harv (link)
- Frolov, Valeri P.; Zelnikov, Andrei (2011), Introduction to Black Hole Physics, Oxford: Oxford University Press, ISBN 978-0-19-969229-3, Zbl 1234.83001CS1 maint: ref=harv (link)
- Hawking, S. W.; Ellis, G. F. R. (1973), Large Scale Structure of space time, Cambridge University Press, ISBN 0-521-09906-4CS1 maint: ref=harv (link)
- Melia, Fulvio (2007), The Galactic Supermassive Black Hole, Princeton U Press, ISBN 978-0-691-13129-0CS1 maint: ref=harv (link)
- Schutz, Bernard F. (2009), A first course in general relativity (lxb. 2), Cambridge University Press, ISBN 0-521-88705-4CS1 maint: ref=harv (link)
- Taylor, Edwin F.; Wheeler, John Archibald (2000), Exploring Black Holes, Addison Wesley Longman, ISBN 0-201-38423-XCS1 maint: ref=harv (link)
- Misner, Charles; Thorne, Kip S.; Wheeler, John (1973), Gravitation, W. H. Freeman and Company, ISBN 0-7167-0344-0CS1 maint: ref=harv (link)
- Wald, Robert M. (1984), General Relativity, University of Chicago Press, ISBN 978-0-226-87033-5CS1 maint: ref=harv (link)
- Wald, Robert M. (1992), Space, Time, and Gravity: The Theory of the Big Bang and Black Holes, University of Chicago Press, ISBN 0-226-87029-4CS1 maint: ref=harv (link)
- Bài tổng quan
- Gallo, Elena; Marolf, Donald (2009), "Resource Letter BH-2: Black Holes", American Journal of Physics, 77 (4): 294, arXiv:0806.2316, Bibcode:2009AmJPh..77..294G, doi:10.1119/1.3056569
- Hughes, Scott A. (2005). Bản mẫu:Citation/make link. arΧiv:hep-ph/0511217 [hep-ph]. Lecture notes from 2005 SLAC Summer Institute.
Liên kết ngoài
(tiếng Việt)
- Hốc đen tại Từ điển Bách khoa Việt Nam
- Hố đen - Don Nardo - Bản dịch tiếng Việt của CLB Thiên văn Bách khoa. Bản gốc tiếng Anh: ISBN 1590181018
- Thông tin thêm về Hố đen vietsciences.free.fr
- S. Hawking, Universe in a nutshell, Bantam, 2001. (Bản dịch tiếng Việt Vũ trụ trong một vỏ hạt)
- S. Hawking, A brief history of time, Bantam, 1986. (Bản dịch tiếng Việt Lược sử thời gian của Cao Chi và Phạm Văn Thiều). Bản PDF trên trang của ĐHTB
- S. Hawking, Does God Play Dice?, public lecture (Chúa có chơi trò súc sắc? Stephen Hawking. Bản dịch tiếng Việt của Zatrach 5/12/2004 từ nguyên văn Does God play Dice?
- GS Hawking nhận sai lầm (về thuyết hố đen của ông) BBC tiếng Việt, 22/7/2004
(tiếng Anh)
- Lỗ đen tại Encyclopædia Britannica
- Black holes & Co. Einstein Online
- Black Holes NASA's Science Mission Directorate (SMD) news
- Frequently Asked Questions (FAQs) on Black Holes. Những câu thường hỏi về hố đen của NASA
- Những câu thường hỏi về hố đen của Đại học California tại Berkeley
- More about the Schwarzschild Geometry Hình học Schwarzschild tại trang của Andrew Hamilton
- Inside black hole Đại học Colorado
- Black Holes: Gravity's Relentless Pull Award-winning interactive multimedia Web site about the physics and astronomy of black holes from the Space Telescope Science Institute
- Tufts University: Student Project (Great Kid's Section)
- Jillian’s Guide to Black Holes
- Universe Today Black hole news stories
- Simulating Extreme Spactimes A Caltech - Cornell project
- Galactic Center Research: Galactic Black Hole disrupts Gas Cloud from Max Plank Institute
- The Largest Black Holes in the Universe (VERSION ONE) ở YouTube SpaceRip tải lên ngày 28-09-2009