Số pi

Số pi là một số vô tỷ và đồng thời là một số siêu việt. Giá trị của số pi là tỷ lệ của chu vi đến đường kính của một đường tròn, thường được lấy gần đúng là 3,14.

Lịch sử

Khái niệm về số pi từ buổi đầu gắn liền với hình học và đặc biệt là với đường tròn. Đường tròn là một trong những đường kỷ hà thường được bắt gặp trong tự nhiên (hình dạng đóa hoa, bong bóng, mống mắt, v.v.) và các thiên thể thường có hình tròn như mặt trời, mặt trăng, cầu vồng, v.v. Các đối tượng này từ thuở sơ khai đã định hình sự đặc biệt của đường tròn đối với con người. Các nền văn minh, văn hóa trong lịch sử đã gắn liền đường tròn với thế giới siêu nhiên.

• 

  Thần Rê trong thần thoại Ai Cập cổ đại với biểu tượng mặt trời hình tròn

• 

  Hình ảnh mặt trời trong văn minh Lưỡng Hà

• 

  Các đường tròn đồng tâm trong hoa văn trên mặt trống đồng Đông Sơn từ văn hóa Đông Sơn

Với vai trò như vậy nên các đề cập về đường tròn trong các tài liệu cổ đã thể hiện sự hiểu biết nhất định về số pi.

Văn minh Lưỡng Hà

Một trong những đề cập đến số pi trong hình học sớm nhất là bài toán "Mở rộng một ngôi làng hình tròn", được ghi chép dưới dạng chữ Cunéiforme trên một tấm đất sét nung từ khu vực Lưỡng Hà vào khoảng năm 1600 TCN.

Mẫu đất sét nung BM 85194

Bài toán được đặt ra như sau : "Một ngôi làng. Một đường tròn có chu vi mà tôi đo được là khoảng 60 đơn vị (cho bán kính r). Từ đường tròn này, tôi di chuyển ra xa với 5 đơn vị và tôi đào một cái hào chạy xung quanh (nghĩa là vẽ một đường tròn đồng tâm với bán kính r+5). Hào sâu 6 đơn vị. Rồi từ hào đó, tôi lại di chuyển ra xa thêm 5 đơn vị nữa, tôi xây một bức lũy (vẽ tiếp một đường tròn đồng tâm với bán kính r+10). Người ta hỏi độ cao, độ sâu của móng và chu vi của bức lũy".

Lời giải cho bài toán được ghi chép như sau : "Khi mà chu vi là một bộ 60 đơn vị (1 shush, người Lưỡng Hà dùng hệ lục thập phân), khoảng vượt (cg. đường kính) là bao nhiêu ? Một phần ba của 60, chu vi, giảm đi, ta thấy 20, 20 là khoảng vượt. 2 lần vòng tròn rộng thêm 5, ta thấy 10. 10 đến 20, khoảng vượt cộng thêm, ta thấy 30, đó là khoảng vượt. Gấp ba lần, ta thấy 1*30 (1 shush và 30 đơn vị, tức là 90 đơn vị), 1*30 là chu vi của lũy".

Cách đặt vấn đề và lời giải này là từ ghi chép rất cổ xưa, khi đó, văn phong và ngôn ngữ là còn chân phương dưới nhận thức hiện đại; tuy nhiên, điểm đặc biệt đáng chú ý là, khi chu vi là 60 thì đường kính sẽ là 1/3 của chu vi, là 20, rồi cộng 2 lần 5 đơn vị cho đường kính 20, được đường kính 30, sau đó lại nhân 3 lần để được chu vi của đường tròn lớn nhất. Điều này có thể được hiểu là, cư dân Lưỡng Hà có thể đã cho rằng tỷ lệ của chu vi đến đường kính của đường tròn là 3, trường hợp này đã được gặp trong nhiều ghi ghép khác. Nói thêm, 3 là tỷ lệ chính xác của chu vi đến đường kính trong trường hợp lục giác đều, người Lưỡng Hà có thể đã cho rằng diện tích hình tròn không lớn hơn diện tích lục giác đều nhiều, và có ít nhất một tấm đất sét nung đã chỉ ra giá trị gần đúng hơn của tỷ lệ này là 3 cộng với 1/8 (3,125).

Văn minh Ai Cập cổ đại

Minh họa cách tính diện tích hình tròn đường kính 9 khet ở cuộn giấy cói Rhind

Nền văn minh Ai Cập cổ đại cùng thời với văn minh Lưỡng Hà (bắt đầu vào khoảng năm 3100 TCN), cũng đã có những ghi chép về các bài toán có liên quan đến đường tròn trong các cuộn giấy cói (papyrus), đặc biệt là cuộn giấy cói Rhind (khoảng năm 1650 TCN). Trong đó có ghi chép về bài toán "Cánh đồng tròn với đường kính 9 khet".

Mẫu giấy cói Rhind ghi lại bài toán đường tròn

Bài toán yêu cầu tính diện tích của một cánh đồng hình tròn với đường kính là 9 khet. Người Ai Cập cổ đại đã đưa ra cách giải như sau : Lấy ra 1/9 của đường kính, là 1. Phần còn lại là 8. Nhân 8 với 8, được 64. Vậy diện tích cánh đồng là 64 setat.

Thực chất, đây là một giải thuật (algorithme) tìm diện tích hơn là công thức bình phương bán kính nhân với một hằng số. Nhìn nhận giải thuật này dưới nhận thức toán học hiện đại, thấy rằng, nó tương đương với việc nhân bình phương của đường kính (D²) với bình phương của 8/9, hay còn là bình phương của bán kính (R²) với 256/81 (3,1604938272).

Diện tích = 8×8 = 8² = 8²×(9/9)² = (8/9)²×D² = (64/81)×D² = (64/81)×(2×R)² = (256/81)×R² ≈ π×R²

Có thể hiểu, đằng sau giải thuật tìm diện tích hình tròn, người Ai Cập cổ đại đã có thể có ý thức về một hằng số. Có nhiều giả thuyết lý giải cho việc người Ai Cập cổ đại tìm ra tỷ lệ 256/81. Tỷ lệ này là một trong những cố gắng đầu tiên trong việc khám phá bản chất của số pi.

Văn minh lưu vực sông Ấn

Nền Văn minh lưu vực sông Ấn (khoảng năm 2600 TCN) cũng đã để lại những ghi chép có liên quan đến số pi, trong đó có tập hướng dẫn Śulba-Sūtras vào khoảng năm 700 TCN. Śulba-Sūtras (Śulba : sợi dây, Sūtras : quy tắc) là một tập hướng dẫn những quy cách xây dựng bệ thờ trong tôn giáo Védisme thời Ấn Độ cổ đại. Do đây là một tập hướng dẫn trong xây dựng hơn là một công trình nghiên cứu toán học nên nó chú trọng về tính xấp xỉ hơn là giá trị đúng của số pi, do đó giá trị của số pi thay đổi từ phương thức xây dựng này sang phương thức khác và thậm chí thay đổi trong cùng một phương thức. Tuy vậy, tập hướng dẫn này cũng đã có những áp dụng rất chính xác trong trường hợp số √2 và trong một số giải pháp hình học khác.

Về số pi, vẫn như các tài liệu cổ của các nền văn minh cùng thời, được ẩn chứa trong các giải thuật để giải quyết các vấn đề về hình học và được thể hiện với văn phong cổ đại. Đầu tiên kể đến là hướng dẫn "Độ dài một sợi tóc" : "1/5 của đường kính được cộng thêm 3 lần đường kính cho ra chu vi của đường tròn. Không còn thừa lại độ dài một sợi tóc". Với hướng dẫn này, số pi đạt giá trị : 3 + 1/5 = 3,2, tuy vẫn còn khá xa giá trị thực của số pi nhưng khá hữu dụng trong công tác xây dựng. Một vài hướng dẫn khác có mang tính chất nghiên cứu như cách để chuyển một hình vuông thành một đường tròn và cách ngược lại, tức là chuyển một đường tròn thành một hình vuông, phương pháp nhắc sau là một phiên bản của vấn đề "Cầu phương hình tròn" (tiếng Pháp : Quadrature du cercle).

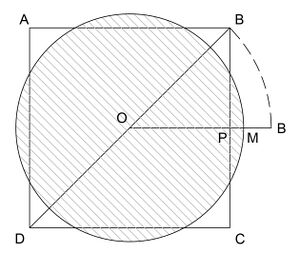
• Chuyển một hình vuông thành một đường tròn : văn bản ghi chép như sau "Nếu người ta muốn chuyển một hình vuông thành một đường tròn, một sợi dây có độ dài là phân nửa của đường xiên hình vuông, dây được căn từ tâm sang bên phải. Cộng thêm 1/3 độ dài còn lại nằm ngoài hình vuông; hình tròn mong muốn đã có". Phương thức được lý giải như sau : hình vuông ở đây có độ dài cạnh là 2, phân nửa đường xiên có giá trị là √2, bán kính của đường tròn cần tìm để cho diện tích của nó đạt 4 là 1 cộng với 1/3 của kết quả lấy căn 2 trừ 1. Số pi đạt được theo phương pháp này là xấp xỉ 3,0883.

Tham khảo

1. Bernard Ycart. La mesure du cercle.
2. Jean-Paul Delahaye. Le fascinant nombre pi. ISBN : 978-2-410-01445-7
3. Sykorova. Charles University, Faculty of Mathematics and Physics, Prague, Czech Republic. ISBN 978-80-7378-139-2